Question Number 17884 by b.e.h.i.8.3.417@gmail.com last updated on 11/Jul/17
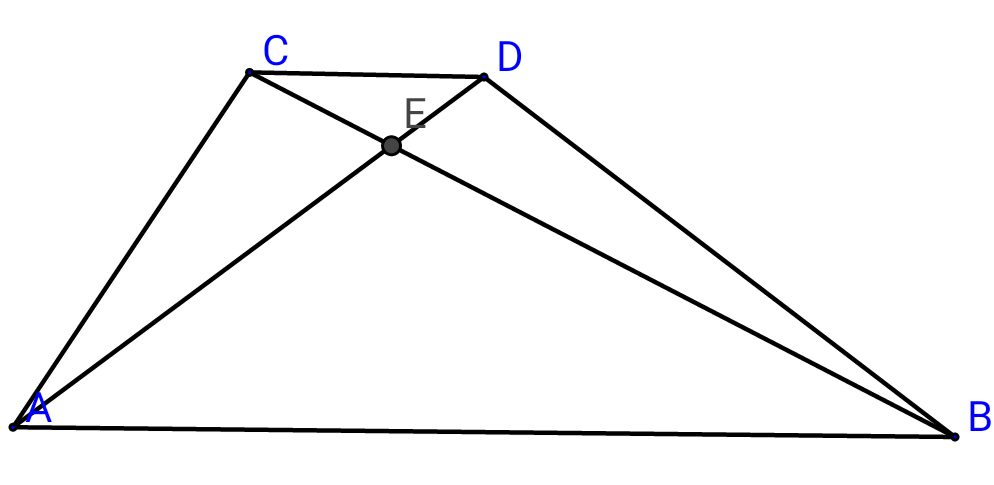
Commented by b.e.h.i.8.3.417@gmail.com last updated on 11/Jul/17

$${diagonals}\:{of}\:{trapezoid}:\:{ABCD},{create} \\ $$$$\mathrm{4}\:{triangles}.{area}\:{of}\:{two}\:{this}\:{triangles} \\ $$$${are}\:{equail}\:{to}:\:{a}^{\mathrm{2}} \:,{and}\:,\:{b}^{\mathrm{2}} . \\ $$$${find}\:{area}\:{of}\:{trapezoid}\:{in}\:{terms}\:{of}:\:{a},{b}. \\ $$$${one}\:{of}\:{diagonals},{cut}\:{another}\:{with} \\ $$$${a}\:\:{given}\:\:{ratio}. \\ $$$${trial}\:{case}: \\ $$$$\:\:\:\:\:\:\:{when}:\:\:\:{S}_{{CDE}} ={a}^{\mathrm{2}} ,\:\:\:{S}_{{ABE}} ={b}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{S}_{{ABCD}} =\left({a}+{b}\right)^{\mathrm{2}} \\ $$
Answered by mrW1 last updated on 12/Jul/17
![let ((CE)/(BE))=((DE)/(AE))=(x/1) case 1: [ABE]=a^2 and [CDE]=b^2 [ACE]=(x/1) a^2 =(1/x) b^2 ⇒x^2 =(b^2 /a^2 ) ⇒x=(b/a) [ABCD]=a^2 +b^2 +2[ACE]=a^2 +b^2 +2 (b/a) a^2 ⇒[ABCD]=(a+b)^2 case 2: [ABE]=a^2 and [ACE]=b^2 (x/1)=(b^2 /a^2 ) [CDE]=(x/1) b^2 =(b^4 /a^2 ) [ABCD]=a^2 +2b^2 +[CDE]=a^2 +2b^2 +(b^4 /a^2 )=((a^4 +2a^2 b^2 +b^4 )/a^2 ) ⇒[ABCD]=(((a^2 +b^2 )^2 )/a^2 )](https://www.tinkutara.com/question/Q17900.png)
$$\mathrm{let}\:\frac{\mathrm{CE}}{\mathrm{BE}}=\frac{\mathrm{DE}}{\mathrm{AE}}=\frac{\mathrm{x}}{\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{1}: \\ $$$$\left[\mathrm{ABE}\right]=\mathrm{a}^{\mathrm{2}} \:\mathrm{and}\:\left[\mathrm{CDE}\right]=\mathrm{b}^{\mathrm{2}} \\ $$$$\left[\mathrm{ACE}\right]=\frac{\mathrm{x}}{\mathrm{1}}\:\mathrm{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{b}}{\mathrm{a}} \\ $$$$\left[\mathrm{ABCD}\right]=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2}\left[\mathrm{ACE}\right]=\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{2}\:\frac{\mathrm{b}}{\mathrm{a}}\:\mathrm{a}^{\mathrm{2}} \\ $$$$\Rightarrow\left[\mathrm{ABCD}\right]=\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{case}\:\mathrm{2}: \\ $$$$\left[\mathrm{ABE}\right]=\mathrm{a}^{\mathrm{2}} \:\mathrm{and}\:\left[\mathrm{ACE}\right]=\mathrm{b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{x}}{\mathrm{1}}=\frac{\mathrm{b}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\left[\mathrm{CDE}\right]=\frac{\mathrm{x}}{\mathrm{1}}\:\mathrm{b}^{\mathrm{2}} =\frac{\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\left[\mathrm{ABCD}\right]=\mathrm{a}^{\mathrm{2}} +\mathrm{2b}^{\mathrm{2}} +\left[\mathrm{CDE}\right]=\mathrm{a}^{\mathrm{2}} +\mathrm{2b}^{\mathrm{2}} +\frac{\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{a}^{\mathrm{4}} +\mathrm{2a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{b}^{\mathrm{4}} }{\mathrm{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\left[\mathrm{ABCD}\right]=\frac{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} } \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 12/Jul/17
![thanks master.one case is remain: [CAE]=a^2 ,[BDE]=b^2 .](https://www.tinkutara.com/question/Q17903.png)
$${thanks}\:{master}.{one}\:{case}\:{is}\:{remain}: \\ $$$$\left[{CAE}\right]={a}^{\mathrm{2}} ,\left[{BDE}\right]={b}^{\mathrm{2}} . \\ $$
Commented by mrW1 last updated on 12/Jul/17
![this is not a possible case, since [CAE]=[BDE] always but [CAE]=[BDE]=b^2 alone is not enough to determine [ABCD] as we can see from case 2.](https://www.tinkutara.com/question/Q17904.png)
$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{possible}\:\mathrm{case}, \\ $$$$\mathrm{since}\:\left[{CAE}\right]=\left[{BDE}\right]\:\mathrm{always} \\ $$$$ \\ $$$$\mathrm{but}\:\left[{CAE}\right]=\left[{BDE}\right]=\mathrm{b}^{\mathrm{2}} \:\mathrm{alone}\:\mathrm{is}\:\mathrm{not}\:\mathrm{enough}\:\mathrm{to} \\ $$$$\mathrm{determine}\:\left[\mathrm{ABCD}\right]\:\mathrm{as}\:\mathrm{we}\:\mathrm{can}\:\mathrm{see}\:\mathrm{from} \\ $$$$\mathrm{case}\:\mathrm{2}. \\ $$
