Question-83542

Question Number 83542 by Power last updated on 03/Mar/20

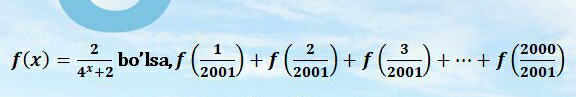
Answered by john santu last updated on 03/Mar/20

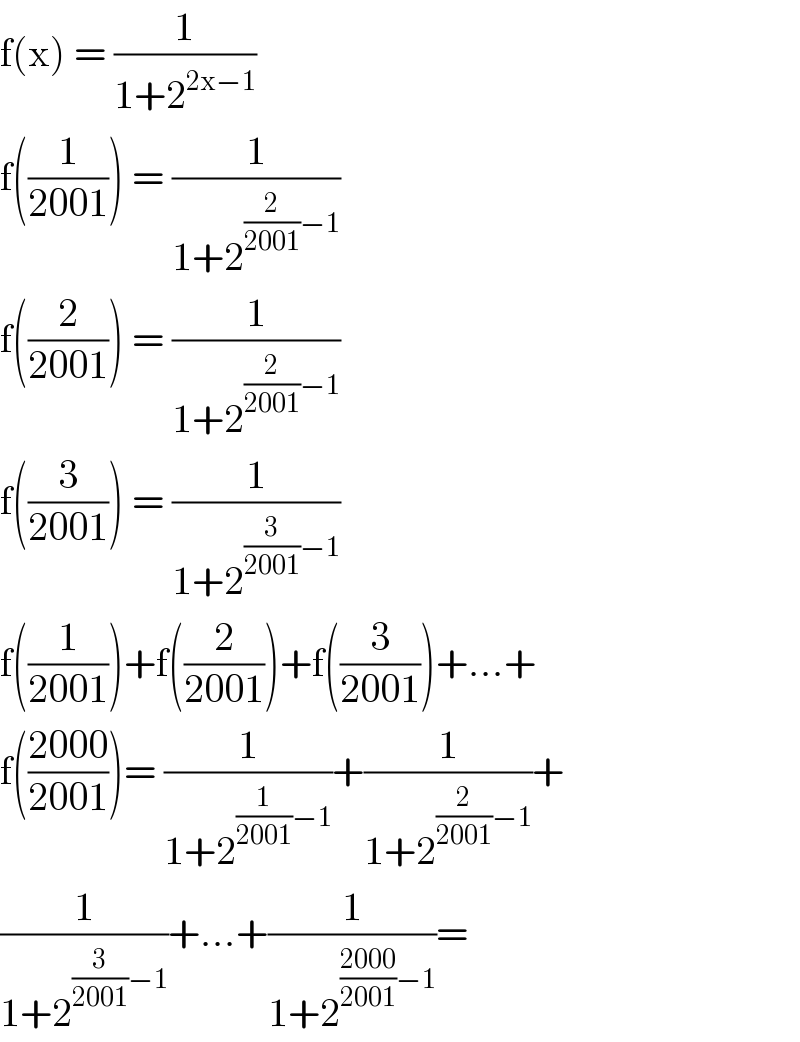
f(x) = (1/(1+2^(2x−1) )) f((1/(2001))) = (1/(1+2^((2/(2001))−1) )) f((2/(2001))) = (1/(1+2^((2/(2001))−1) )) f((3/(2001))) = (1/(1+2^((3/(2001))−1) )) f((1/(2001)))+f((2/(2001)))+f((3/(2001)))+...+ f(((2000)/(2001)))= (1/(1+2^((1/(2001))−1) ))+(1/(1+2^((2/(2001))−1) ))+ (1/(1+2^((3/(2001))−1) ))+...+(1/(1+2^(((2000)/(2001))−1) ))=

$$\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{2x}−\mathrm{1}} } \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2001}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{2001}}−\mathrm{1}} } \\ $$$$\mathrm{f}\left(\frac{\mathrm{2}}{\mathrm{2001}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{2001}}−\mathrm{1}} } \\ $$$$\mathrm{f}\left(\frac{\mathrm{3}}{\mathrm{2001}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2001}}−\mathrm{1}} } \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2001}}\right)+\mathrm{f}\left(\frac{\mathrm{2}}{\mathrm{2001}}\right)+\mathrm{f}\left(\frac{\mathrm{3}}{\mathrm{2001}}\right)+…+ \\ $$$$\mathrm{f}\left(\frac{\mathrm{2000}}{\mathrm{2001}}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2001}}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{2001}}−\mathrm{1}} }+ \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2001}}−\mathrm{1}} }+…+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{\mathrm{2000}}{\mathrm{2001}}−\mathrm{1}} }=\:\:\: \\ $$

Commented by john santu last updated on 03/Mar/20

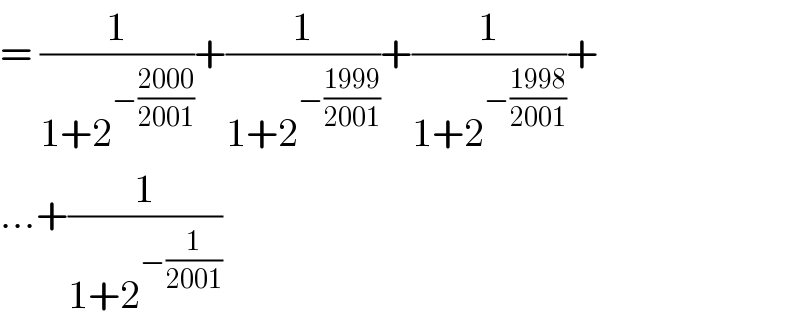
= (1/(1+2^(−((2000)/(2001))) ))+(1/(1+2^(−((1999)/(2001))) ))+(1/(1+2^(−((1998)/(2001))) ))+ ...+(1/(1+2^(−(1/(2001))) ))

$$=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\frac{\mathrm{2000}}{\mathrm{2001}}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\frac{\mathrm{1999}}{\mathrm{2001}}} }+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\frac{\mathrm{1998}}{\mathrm{2001}}} }+ \\ $$$$…+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2001}}} } \\ $$

Answered by mahdi last updated on 03/Mar/20

if m+n=1⇒ f(m)+f(n)=(2/(4^m +2))+(2/(4^n +2))=((2(4^n +2)+2(4^m +2))/((4^m +2)(4^n +2)))= ((8+2(4^m +4^n ))/(4+4^m ×4^n +2(4^m +4^n )))=1 (4^m ×4^n =4^(m+n) =4^1 ) ⇒[f((1/(2001)))+f(((2000)/(2001)))]+[f((2/(2001)))+f(((1999)/(2001)))]+ ...+[f(((1000)/(2001)))+f(((1001)/(2001)))]=1000×1=1000

$$\mathrm{if}\:\:\:\mathrm{m}+\mathrm{n}=\mathrm{1}\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{m}\right)+\mathrm{f}\left(\mathrm{n}\right)=\frac{\mathrm{2}}{\mathrm{4}^{\mathrm{m}} +\mathrm{2}}+\frac{\mathrm{2}}{\mathrm{4}^{\mathrm{n}} +\mathrm{2}}=\frac{\mathrm{2}\left(\mathrm{4}^{\mathrm{n}} +\mathrm{2}\right)+\mathrm{2}\left(\mathrm{4}^{\mathrm{m}} +\mathrm{2}\right)}{\left(\mathrm{4}^{\mathrm{m}} +\mathrm{2}\right)\left(\mathrm{4}^{\mathrm{n}} +\mathrm{2}\right)}= \\ $$$$\frac{\mathrm{8}+\mathrm{2}\left(\mathrm{4}^{\mathrm{m}} +\mathrm{4}^{\mathrm{n}} \right)}{\mathrm{4}+\mathrm{4}^{\mathrm{m}} ×\mathrm{4}^{\mathrm{n}} +\mathrm{2}\left(\mathrm{4}^{\mathrm{m}} +\mathrm{4}^{\mathrm{n}} \right)}=\mathrm{1}\:\:\:\:\left(\mathrm{4}^{\mathrm{m}} ×\mathrm{4}^{\mathrm{n}} =\mathrm{4}^{\mathrm{m}+\mathrm{n}} =\mathrm{4}^{\mathrm{1}} \right) \\ $$$$\Rightarrow\left[\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2001}}\right)+\mathrm{f}\left(\frac{\mathrm{2000}}{\mathrm{2001}}\right)\right]+\left[\mathrm{f}\left(\frac{\mathrm{2}}{\mathrm{2001}}\right)+\mathrm{f}\left(\frac{\mathrm{1999}}{\mathrm{2001}}\right)\right]+ \\ $$$$…+\left[\mathrm{f}\left(\frac{\mathrm{1000}}{\mathrm{2001}}\right)+\mathrm{f}\left(\frac{\mathrm{1001}}{\mathrm{2001}}\right)\right]=\mathrm{1000}×\mathrm{1}=\mathrm{1000} \\ $$

Commented by Power last updated on 03/Mar/20

$$\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply