Question Number 149151 by mathdanisur last updated on 03/Aug/21
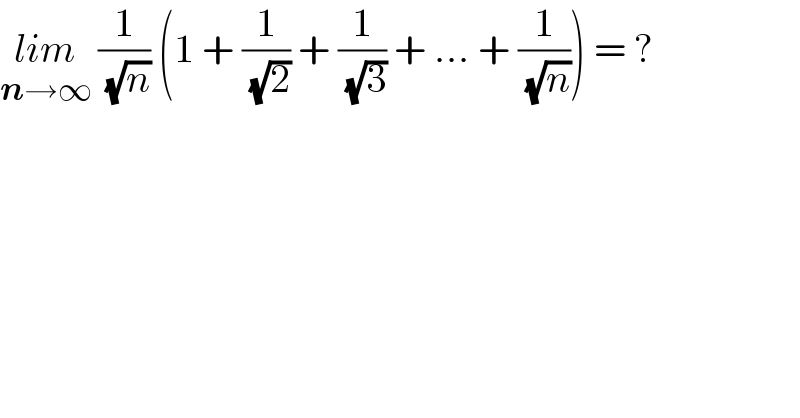
$$\underset{\boldsymbol{{n}}\rightarrow\infty} {{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{n}}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\:…\:+\:\frac{\mathrm{1}}{\:\sqrt{{n}}}\right)\:=\:? \\ $$
Answered by Kamel last updated on 03/Aug/21
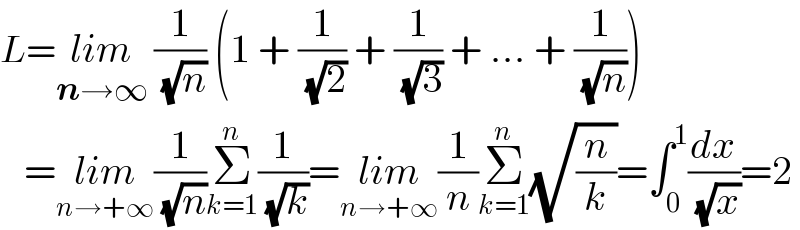
$${L}=\underset{\boldsymbol{{n}}\rightarrow\infty} {{lim}}\:\frac{\mathrm{1}}{\:\sqrt{{n}}}\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\:…\:+\:\frac{\mathrm{1}}{\:\sqrt{{n}}}\right)\: \\ $$$$\:\:\:=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}}}=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{\frac{{n}}{{k}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}}=\mathrm{2} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
Answered by puissant last updated on 03/Aug/21
![=lim_(n→∞) (1/( (√n))) Σ_(k=1) ^n (√(1/k)) =lim_(n→∞) (1/n) Σ_(k=1) ^n (√((n/k) ))= f((k/n)) d′apre^� s riemann, on a: =∫_0 ^1 (1/( (√x))) dx = ∫_0 ^1 x^(−(1/2)) dx = 2[(√x)]_0 ^1 =2..](https://www.tinkutara.com/question/Q149162.png)
$$=\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\frac{\mathrm{1}}{\mathrm{k}}} \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{n}}\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\frac{\mathrm{n}}{\mathrm{k}}\:}=\:\mathrm{f}\left(\frac{\mathrm{k}}{\mathrm{n}}\right) \\ $$$$\mathrm{d}'\mathrm{apr}\grave {\mathrm{e}s}\:\mathrm{riemann},\:\mathrm{on}\:\mathrm{a}: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{x}}}\:\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dx}\:=\:\mathrm{2}\left[\sqrt{\mathrm{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}.. \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
Answered by Rachid last updated on 03/Aug/21
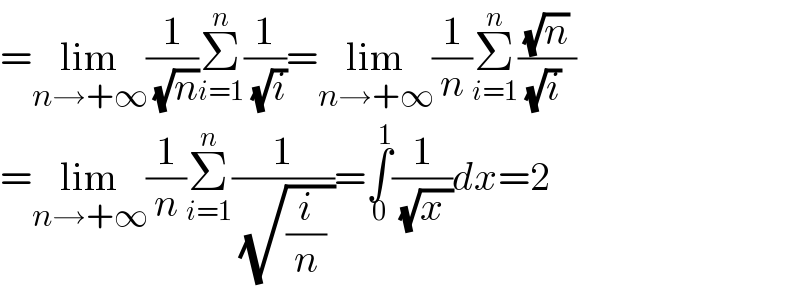
$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{{n}}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{i}}}=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\sqrt{{n}}}{\:\sqrt{{i}}\:\:} \\ $$$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\frac{{i}}{{n}}\:}}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}}{\:\sqrt{{x}\:}}{dx}=\mathrm{2} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
Answered by dumitrel last updated on 03/Aug/21

$${use}\:\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}<\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}<\frac{\mathrm{1}}{\:\sqrt{{n}}} \\ $$
Commented by mathdanisur last updated on 03/Aug/21

$${Thank}\:{You}\:{Ser} \\ $$
