Menu Close

Question-18111

Tinku Tara 0 Comments
Pin




Question Number 18111 by ajfour last updated on 15/Jul/17
Commented by ajfour last updated on 15/Jul/17
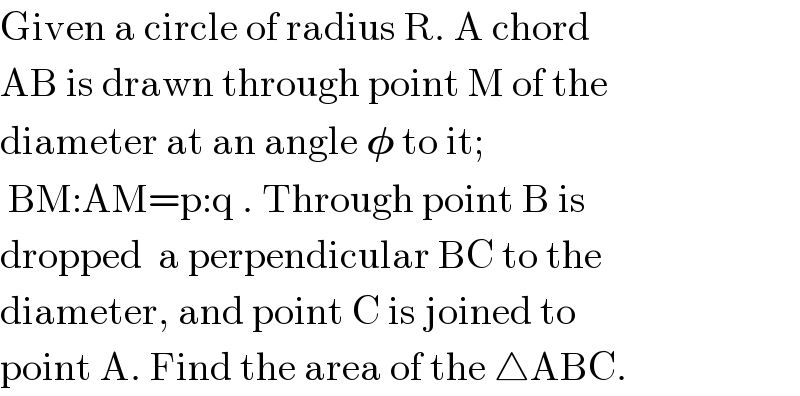
Given a circle of radius R. A chord AB is drawn through point M of the diameter at an angle 𝛗 to it; BM:AM=p:q . Through point B is dropped a perpendicular BC to the diameter, and point C is joined to point A. Find the area of the △ABC.
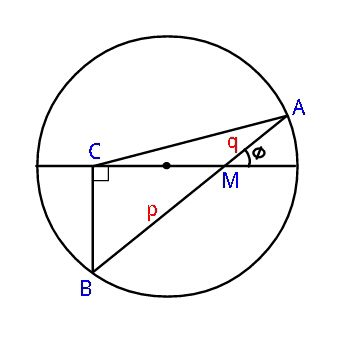
$$\mathrm{Given}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{R}.\:\mathrm{A}\:\mathrm{chord} \\ $$$$\mathrm{AB}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{through}\:\mathrm{point}\:\mathrm{M}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{diameter}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angle}\:\boldsymbol{\phi}\:\mathrm{to}\:\mathrm{it}; \\ $$$$\:\mathrm{BM}:\mathrm{AM}=\mathrm{p}:\mathrm{q}\:.\:\mathrm{Through}\:\mathrm{point}\:\mathrm{B}\:\mathrm{is} \\ $$$$\mathrm{dropped}\:\:\mathrm{a}\:\mathrm{perpendicular}\:\mathrm{BC}\:\mathrm{to}\:\mathrm{the} \\ $$$$\mathrm{diameter},\:\mathrm{and}\:\mathrm{point}\:\mathrm{C}\:\mathrm{is}\:\mathrm{joined}\:\mathrm{to} \\ $$$$\mathrm{point}\:\mathrm{A}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\bigtriangleup\mathrm{ABC}. \\ $$
Commented by ajfour last updated on 16/Jul/17
Commented by ajfour last updated on 16/Jul/17
let O be centre of circle. length of chird AB=l construct OF ⊥ to chord AB. let its length is d. let ((AM)/(AM+BM))=λ =(q/(p+q)) ⇒ ((AM)/(AB))=λ AM=λl , BM=(1−λl) Also AM=AF−FM λl=(l/2)−dcot φ ..(i) BM=BF+FM (1−λ)l=(l/2)+dcot φ ...(ii) (ii)−(i) gives: (1−2λ)l=2dcot φ ⇒ tan^2 φ(1−2λ)l^2 =4(R^2 −(l^2 /4)) l^2 =((4R^2 )/(1+(1−2λ)^2 tan^2 φ)) S_(ABC) =(1/2)×BC×(AM+BM)cos φ =(1/2)(BMsin φ)lcos φ =(1/4)(1−λ)l^2 sin 2φ =(1/4)((p/(p+q))).[((4R^2 )/(1+(((p−q)/(p+q)))^2 tan^2 φ))] S_(ABC) =((p(p+q)R^2 sin 2φ)/((p+q)^2 +(p−q)^2 tan^2 φ)) .
$$\mathrm{let}\:\mathrm{O}\:\mathrm{be}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{circle}. \\ $$$$\mathrm{length}\:\mathrm{of}\:\mathrm{chird}\:\mathrm{AB}={l} \\ $$$$\mathrm{construct}\:\mathrm{OF}\:\bot\:\mathrm{to}\:\mathrm{chord}\:\mathrm{AB}. \\ $$$$\mathrm{let}\:\mathrm{its}\:\mathrm{length}\:\mathrm{is}\:\mathrm{d}. \\ $$$$\mathrm{let}\:\:\frac{\mathrm{AM}}{\mathrm{AM}+\mathrm{BM}}=\lambda\:=\frac{\mathrm{q}}{\mathrm{p}+\mathrm{q}}\:\Rightarrow\:\frac{\mathrm{AM}}{\mathrm{AB}}=\lambda \\ $$$$\:\:\:\mathrm{AM}=\lambda{l}\:\:\:,\:\:\:\mathrm{BM}=\left(\mathrm{1}−\lambda{l}\right) \\ $$$$\mathrm{Also}\:\:\:\:\:\mathrm{AM}=\mathrm{AF}−\mathrm{FM} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\lambda{l}=\frac{{l}}{\mathrm{2}}−\mathrm{dcot}\:\phi\:\:\:..\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{BM}=\mathrm{BF}+\mathrm{FM} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{1}−\lambda\right){l}=\frac{{l}}{\mathrm{2}}+\mathrm{dcot}\:\phi\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{ii}\right)−\left(\mathrm{i}\right)\:\mathrm{gives}: \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{1}−\mathrm{2}\lambda\right){l}=\mathrm{2dcot}\:\phi \\ $$$$\Rightarrow\:\mathrm{tan}\:^{\mathrm{2}} \phi\left(\mathrm{1}−\mathrm{2}\lambda\right){l}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{R}^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:{l}^{\mathrm{2}} =\frac{\mathrm{4R}^{\mathrm{2}} }{\mathrm{1}+\left(\mathrm{1}−\mathrm{2}\lambda\right)^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \phi} \\ $$$$\mathrm{S}_{\mathrm{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{BC}×\left(\mathrm{AM}+\mathrm{BM}\right)\mathrm{cos}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{BMsin}\:\phi\right){l}\mathrm{cos}\:\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}−\lambda\right){l}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\phi \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{p}}{\mathrm{p}+\mathrm{q}}\right).\left[\frac{\mathrm{4R}^{\mathrm{2}} }{\mathrm{1}+\left(\frac{\mathrm{p}−\mathrm{q}}{\mathrm{p}+\mathrm{q}}\right)^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \phi}\right] \\ $$$$\:\:\mathrm{S}_{\mathrm{ABC}} =\frac{\mathrm{p}\left(\mathrm{p}+\mathrm{q}\right)\mathrm{R}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\phi}{\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} +\left(\mathrm{p}−\mathrm{q}\right)^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \phi}\:. \\ $$
Answered by b.e.h.i.8.3.417@gmail.com last updated on 15/Jul/17
AB=a ((BM)/(AM))=(p/q)⇒((BM)/(BM+AM))=(p/(p+q))⇒BM=a.(p/(p+q)) cosϕ=((CM)/(MB))⇒CM=((ap)/((p+q).cosϕ)) CB=((ap)/((p+q).sinϕ)) AM=a−((ap)/(p+q))⇒AM=((aq)/(p+q)) S_(ABC) =(1/2)BC.CM+(1/2).CM.AM.sin(180−ϕ)= =(1/2)(BC+AM.sinϕ).CM= =(1/2)(((ap)/((p+q).sinϕ))+((aq)/((p+q))).sinϕ).((ap)/((p+q).cosϕ))= =((a^2 .p(p+q.sin^2 ϕ))/((p+q)^2 .sin2ϕ))=p.((p+q.sin^2 ϕ)/(sin2ϕ)). if you mean: p+q=a.
$${AB}={a} \\ $$$$\frac{{BM}}{{AM}}=\frac{{p}}{{q}}\Rightarrow\frac{{BM}}{{BM}+{AM}}=\frac{{p}}{{p}+{q}}\Rightarrow{BM}={a}.\frac{{p}}{{p}+{q}} \\ $$$${cos}\varphi=\frac{{CM}}{{MB}}\Rightarrow{CM}=\frac{{ap}}{\left({p}+{q}\right).{cos}\varphi} \\ $$$${CB}=\frac{{ap}}{\left({p}+{q}\right).{sin}\varphi} \\ $$$${AM}={a}−\frac{{ap}}{{p}+{q}}\Rightarrow{AM}=\frac{{aq}}{{p}+{q}} \\ $$$${S}_{{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}{BC}.{CM}+\frac{\mathrm{1}}{\mathrm{2}}.{CM}.{AM}.{sin}\left(\mathrm{180}−\varphi\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({BC}+{AM}.{sin}\varphi\right).{CM}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{ap}}{\left({p}+{q}\right).{sin}\varphi}+\frac{{aq}}{\left({p}+{q}\right)}.{sin}\varphi\right).\frac{{ap}}{\left({p}+{q}\right).{cos}\varphi}= \\ $$$$=\frac{{a}^{\mathrm{2}} .{p}\left({p}+{q}.{sin}^{\mathrm{2}} \varphi\right)}{\left({p}+{q}\right)^{\mathrm{2}} .{sin}\mathrm{2}\varphi}={p}.\frac{{p}+{q}.{sin}^{\mathrm{2}} \varphi}{{sin}\mathrm{2}\varphi}. \\ $$$${if}\:{you}\:{mean}:\:\:{p}+{q}={a}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *