Question Number 149205 by ArielVyny last updated on 03/Aug/21
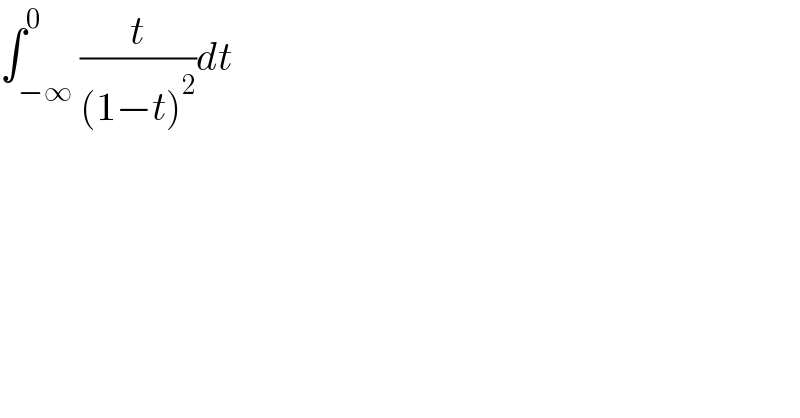
$$\int_{−\infty} ^{\mathrm{0}} \frac{{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt} \\ $$
Answered by MJS_new last updated on 03/Aug/21
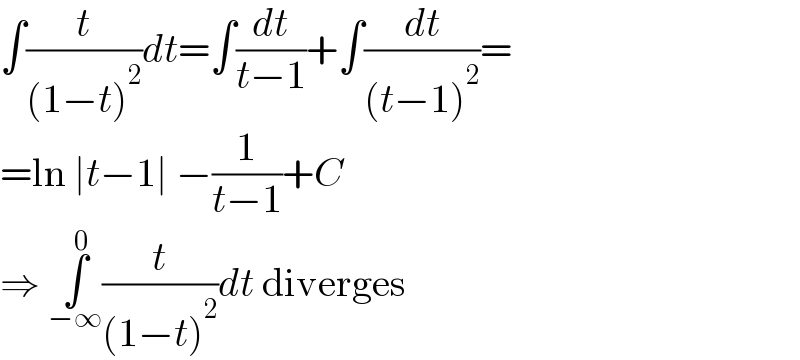
$$\int\frac{{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt}=\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\mathrm{ln}\:\mid{t}−\mathrm{1}\mid\:−\frac{\mathrm{1}}{{t}−\mathrm{1}}+{C} \\ $$$$\Rightarrow\:\underset{−\infty} {\overset{\mathrm{0}} {\int}}\frac{{t}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt}\:\mathrm{diverges} \\ $$
