Question Number 18185 by Tinkutara last updated on 16/Jul/17
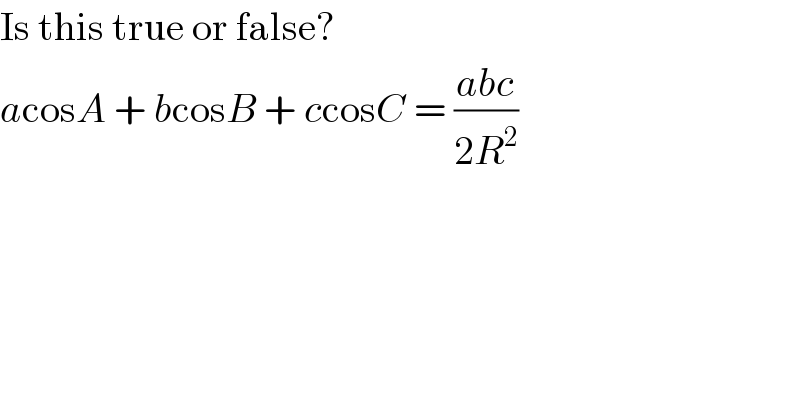
$$\mathrm{Is}\:\mathrm{this}\:\mathrm{true}\:\mathrm{or}\:\mathrm{false}? \\ $$$${a}\mathrm{cos}{A}\:+\:{b}\mathrm{cos}{B}\:+\:{c}\mathrm{cos}{C}\:=\:\frac{{abc}}{\mathrm{2}{R}^{\mathrm{2}} } \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 16/Jul/17

$${yes}.\:{it}\:{is}\:{true}. \\ $$$${in}\:{triangle}\:{ABC},{draw}\:{altitudes}\:{of} \\ $$$${triangle}.{connecting}\:{foots}\:{of}\:{this}\:{altitudes}, \\ $$$${makes}\:{a}\:{triangle}\:{that}\:{called}\:{as}\::{altitudial} \\ $$$${triangle}\:{of}\:{ABC}. \\ $$$${let}\:{call}\:{altitudial}\:{triangle}\:{of}\:{ABC},{by} \\ $$$${M}\overset{\Delta} {{N}P}.{in}\:{triangle}\:{MNP},{we}\:{can}\:{easily} \\ $$$${prove}\:{below}\:{relations}: \\ $$$$\left.\mathrm{1}\right)\measuredangle{M}=\pi−\mathrm{2}{A},\measuredangle{N}=\pi−\mathrm{2}{B},\measuredangle{P}=\pi−\mathrm{2}{C} \\ $$$$\left.\mathrm{2}\right){PN}={a}.{cosA},{PM}={b}.{cosB},{MN}={c}.{cosC} \\ $$$$\left.\mathrm{3}\right){R}'=\frac{{R}}{\mathrm{2}},{r}'=\mathrm{4}{R}'.{sin}\frac{{M}}{\mathrm{2}}{sin}\frac{{N}}{\mathrm{2}}{sin}\frac{{P}}{\mathrm{2}}= \\ $$$$=\mathrm{2}{R}.{cosA}.{cosB}.{cosC} \\ $$$$\left.\mathrm{4}\right){S}_{{MNP}} =\mathrm{2}{S}_{{ABC}} .{cosA}.{cosB}.{cosC} \\ $$$$\left.\mathrm{5}\right){p}'=\mathrm{4}{R}'.{cos}\frac{{M}}{\mathrm{2}}.{cos}\frac{{N}}{\mathrm{2}}.{cos}\frac{{P}}{\mathrm{2}}= \\ $$$$=\mathrm{2}{R}.{sinA}.{sinB}.{sinC}=\frac{{S}}{{R}} \\ $$$${now},{the}\:{LHS},{in}\:{fact},{is}\:{the}\:{premeter}\:{of} \\ $$$${the}\:{altitudial}\:{triangle}\:{of}\:{ABC}.{in}\:{part} \\ $$$$\mathrm{5},{we}\:{show}\:{that}:{p}'=\frac{{S}}{{R}},{and}\:{so}: \\ $$$${LHS}=\mathrm{2}{p}'=\mathrm{2}.\frac{{S}}{{R}}.{but}\:: \\ $$$${RHS}=\frac{\mathrm{4}{RS}}{\mathrm{2}{R}^{\mathrm{2}} }=\mathrm{2}.\frac{{S}}{{R}}.{Hence}:{LHS}={RHS}. \\ $$$${note}: \\ $$$$\left.\mathrm{1}\right){S}_{{ABC}} =\frac{\mathrm{1}}{\mathrm{2}}{ab}.{sinC}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{R}.{sinA}.\mathrm{2}{R}.{sinB}.{sinC}= \\ $$$$=\mathrm{2}{R}^{\mathrm{2}} .\Pi{sinA} \\ $$$$\left.\mathrm{2}\right){MN}^{\mathrm{2}} ={CM}^{\mathrm{2}} +{CN}^{\mathrm{2}} −\mathrm{2}.{CM}.{CN}.{cosC}= \\ $$$$=\left({b}.{cosC}\right)^{\mathrm{2}} +\left({a}.{cosC}\right)^{\mathrm{2}} −\mathrm{2}{abcos}^{\mathrm{2}} {C}.{cosC}= \\ $$$$=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}.{cosC}\right).{cos}^{\mathrm{2}} {C}={c}^{\mathrm{2}} .{cos}^{\mathrm{2}} {C} \\ $$$$\Rightarrow{MN}={c}.{cosC}. \\ $$$$\left.\mathrm{3}\right){S}_{{MNP}} =\frac{\mathrm{1}}{\mathrm{2}}.{MN}.{NP}.{sinN}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.{c}.{cosC}.{a}.{cosA}.{sin}\left(\pi−\mathrm{2}{B}\right)= \\ $$$$={ac}.{cosA}.{cosC}.{sinB}.{cosB}= \\ $$$$=\frac{{abc}}{\mathrm{2}{R}}.{cosA}.{cosB}.{cosC}=\mathrm{2}{S}.\Pi{cosA}. \\ $$$$\left.\mathrm{4}\right){R}'=\frac{{PN}}{\mathrm{2}{sinP}}=\frac{{a}.{cosA}}{\mathrm{2}{sin}\left(\mathrm{180}−\mathrm{2}{A}\right)}= \\ $$$$=\frac{{acosA}}{\mathrm{2}×\mathrm{2}{sinA}.{cosA}}=\frac{{a}}{\mathrm{4}{sinA}}=\frac{{R}}{\mathrm{2}} \\ $$
Commented by Tinkutara last updated on 17/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
