Question Number 83782 by jagoll last updated on 06/Mar/20
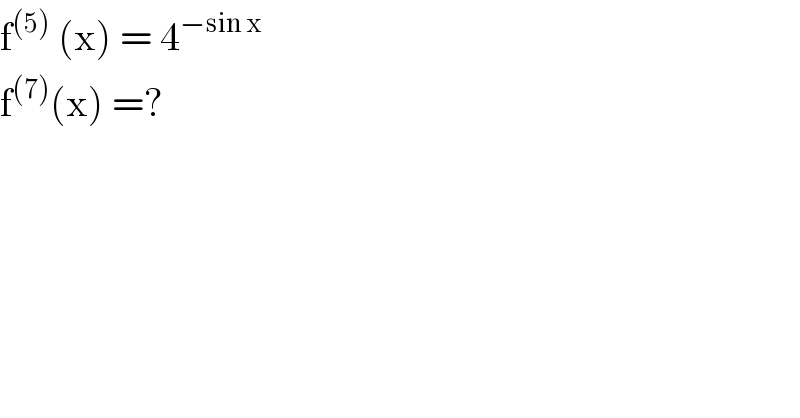
$$\mathrm{f}^{\left(\mathrm{5}\right)} \:\left(\mathrm{x}\right)\:=\:\mathrm{4}^{−\mathrm{sin}\:\mathrm{x}} \\ $$$$\mathrm{f}^{\left(\mathrm{7}\right)} \left(\mathrm{x}\right)\:=?\: \\ $$
Commented by john santu last updated on 06/Mar/20
![f^((n)) (x) = [ f^((n−1)) (x) ]′ f^((6)) (x) = [ f^((5)) (x)] ′ = −cos x. 4^(−sin x) . ln (4) f^((7)) (x)= ln(4) [ sin x. 4^(−sin x) +ln(4) cos^2 x.4^(−sin x) ]](https://www.tinkutara.com/question/Q83783.png)
$$\mathrm{f}^{\left(\mathrm{n}\right)} \left({x}\right)\:=\:\left[\:\mathrm{f}^{\left(\mathrm{n}−\mathrm{1}\right)} \left({x}\right)\:\right]' \\ $$$$\mathrm{f}^{\left(\mathrm{6}\right)} \left({x}\right)\:=\:\left[\:\mathrm{f}^{\left(\mathrm{5}\right)} \:\left({x}\right)\right]\:'\:=\:−\mathrm{cos}\:{x}.\:\mathrm{4}^{−\mathrm{sin}\:{x}} .\:\mathrm{ln}\:\left(\mathrm{4}\right) \\ $$$$\mathrm{f}^{\left(\mathrm{7}\right)} \left({x}\right)=\:\mathrm{ln}\left(\mathrm{4}\right)\:\left[\:\mathrm{sin}\:{x}.\:\mathrm{4}^{−\mathrm{sin}\:{x}} \:+\mathrm{ln}\left(\mathrm{4}\right)\:\mathrm{cos}\:^{\mathrm{2}} {x}.\mathrm{4}^{−\mathrm{sin}\:{x}} \:\right] \\ $$
