Question Number 83919 by john santu last updated on 08/Mar/20
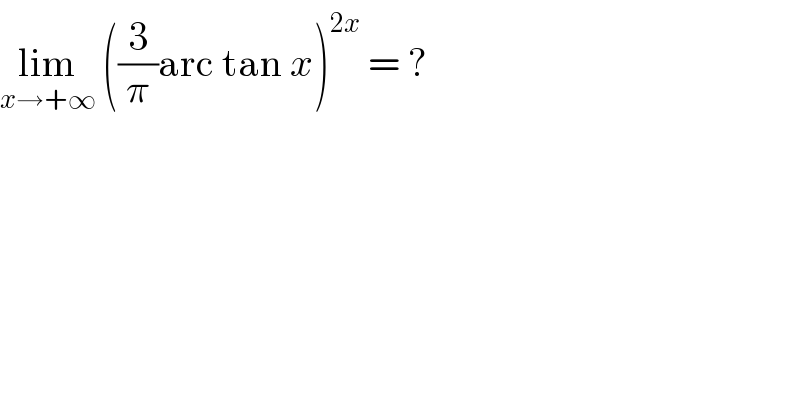
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{3}}{\pi}\mathrm{arc}\:\mathrm{tan}\:{x}\right)^{\mathrm{2}{x}} \:=\:? \\ $$
Commented by john santu last updated on 08/Mar/20
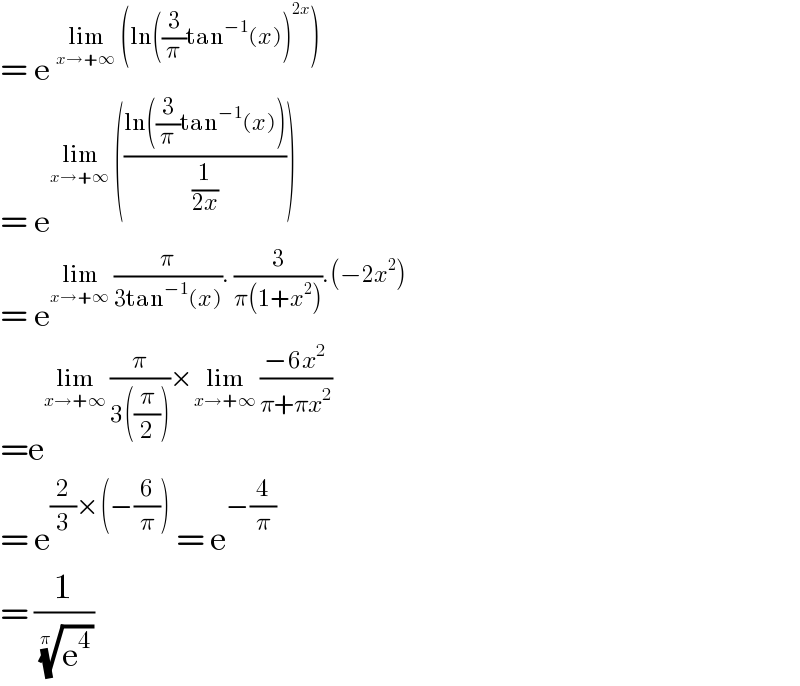
$$=\:\mathrm{e}\:^{\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left(\mathrm{ln}\left(\frac{\mathrm{3}}{\pi}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}{x}} \right)} \\ $$$$=\:\mathrm{e}^{\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{ln}\left(\frac{\mathrm{3}}{\pi}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)}{\frac{\mathrm{1}}{\mathrm{2}{x}}}\right)} \\ $$$$=\:\mathrm{e}^{\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\pi}{\mathrm{3tan}^{−\mathrm{1}} \left({x}\right)}.\:\frac{\mathrm{3}}{\pi\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}.\left(−\mathrm{2}{x}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{e}^{\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\pi}{\mathrm{3}\left(\frac{\pi}{\mathrm{2}}\right)}×\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{−\mathrm{6}{x}^{\mathrm{2}} }{\pi+\pi{x}^{\mathrm{2}} }} \\ $$$$=\:\mathrm{e}^{\frac{\mathrm{2}}{\mathrm{3}}×\left(−\frac{\mathrm{6}}{\pi}\right)} \:=\:\mathrm{e}^{−\frac{\mathrm{4}}{\pi}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt[{\pi\:\:}]{\mathrm{e}^{\mathrm{4}} }}\: \\ $$
