Question Number 67102 by TawaTawa last updated on 22/Aug/19
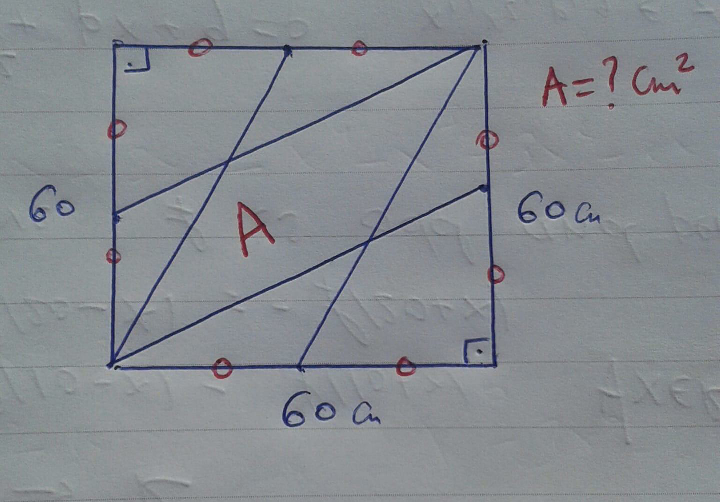
Answered by mr W last updated on 23/Aug/19
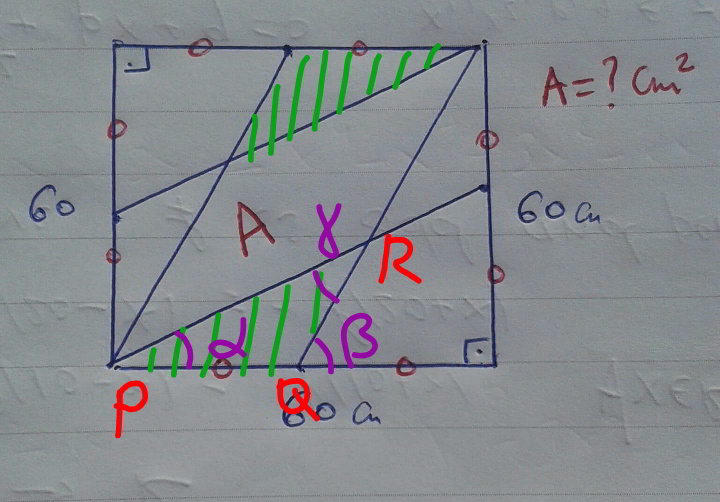
Commented by mr W last updated on 23/Aug/19
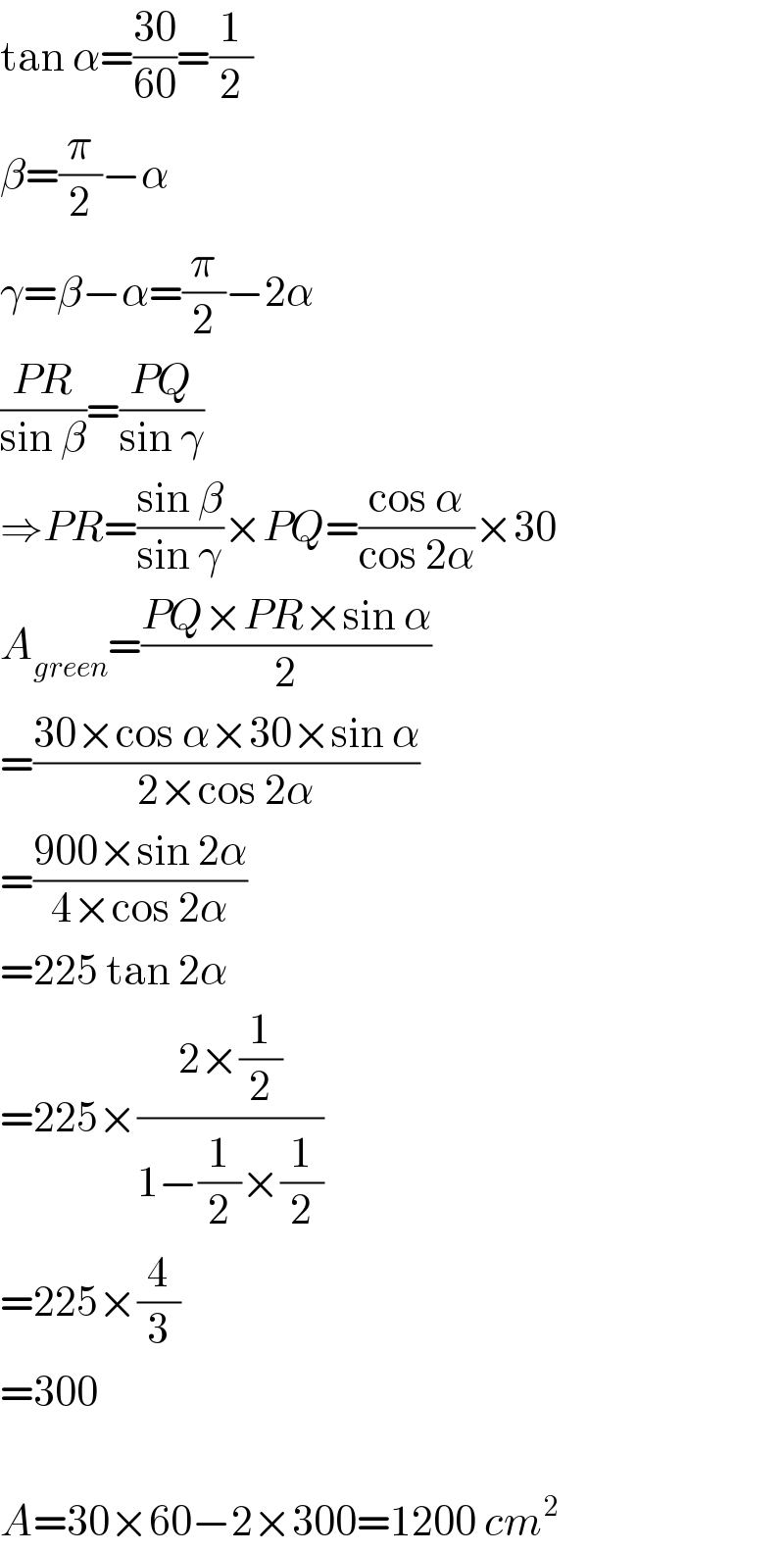
$$\mathrm{tan}\:\alpha=\frac{\mathrm{30}}{\mathrm{60}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\gamma=\beta−\alpha=\frac{\pi}{\mathrm{2}}−\mathrm{2}\alpha \\ $$$$\frac{{PR}}{\mathrm{sin}\:\beta}=\frac{{PQ}}{\mathrm{sin}\:\gamma} \\ $$$$\Rightarrow{PR}=\frac{\mathrm{sin}\:\beta}{\mathrm{sin}\:\gamma}×{PQ}=\frac{\mathrm{cos}\:\alpha}{\mathrm{cos}\:\mathrm{2}\alpha}×\mathrm{30} \\ $$$${A}_{{green}} =\frac{{PQ}×{PR}×\mathrm{sin}\:\alpha}{\mathrm{2}} \\ $$$$=\frac{\mathrm{30}×\mathrm{cos}\:\alpha×\mathrm{30}×\mathrm{sin}\:\alpha}{\mathrm{2}×\mathrm{cos}\:\mathrm{2}\alpha} \\ $$$$=\frac{\mathrm{900}×\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{4}×\mathrm{cos}\:\mathrm{2}\alpha} \\ $$$$=\mathrm{225}\:\mathrm{tan}\:\mathrm{2}\alpha \\ $$$$=\mathrm{225}×\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{225}×\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$=\mathrm{300} \\ $$$$ \\ $$$${A}=\mathrm{30}×\mathrm{60}−\mathrm{2}×\mathrm{300}=\mathrm{1200}\:{cm}^{\mathrm{2}} \\ $$
Commented by mr W last updated on 23/Aug/19

$${alternative}: \\ $$$${let}\:{P}={origin} \\ $$$${eqn}.\:{line}\:{PR}: \\ $$$${y}=\frac{{x}}{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{line}\:{QR}: \\ $$$$\frac{{y}−\mathrm{0}}{\mathrm{60}−\mathrm{0}}=\frac{{x}−\mathrm{30}}{\mathrm{60}−\mathrm{30}} \\ $$$$\Rightarrow{y}=\mathrm{2}{x}−\mathrm{60} \\ $$$${intersection}\:{R}: \\ $$$$\frac{{x}}{\mathrm{2}}=\mathrm{2}{x}−\mathrm{60} \\ $$$$\Rightarrow{x}_{{R}} ={x}=\mathrm{40} \\ $$$$\Rightarrow{y}_{{R}} =\frac{\mathrm{40}}{\mathrm{2}}=\mathrm{20} \\ $$$${A}_{{green}} =\frac{{PQ}×{y}_{{R}} }{\mathrm{2}}=\frac{\mathrm{30}×\mathrm{20}}{\mathrm{2}}=\mathrm{300} \\ $$$${A}=\mathrm{30}×\mathrm{60}−\mathrm{2}×\mathrm{300}=\mathrm{1200}\:{cm}^{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
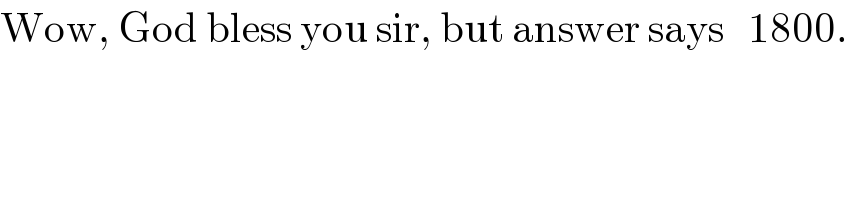
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{answer}\:\mathrm{says}\:\:\:\mathrm{1800}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19

$$\mathrm{That}\:\mathrm{means}\:\mathrm{they}\:\mathrm{are}\:\mathrm{wrong}.\:\:\mathrm{I}\:\mathrm{will}\:\mathrm{use}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 23/Aug/19
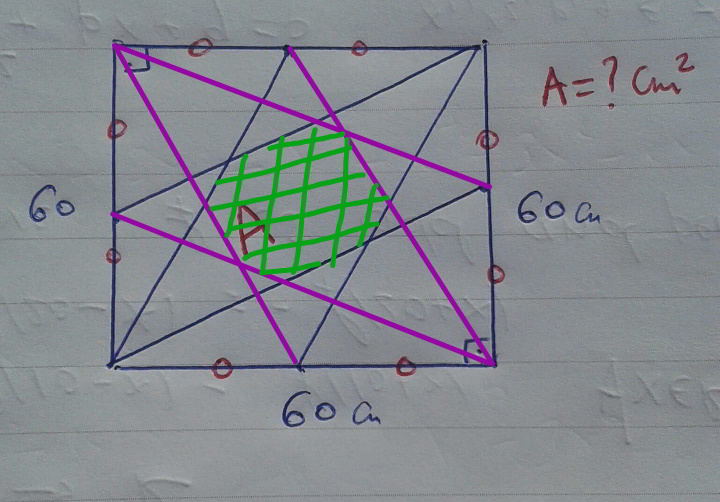
Commented by mr W last updated on 23/Aug/19
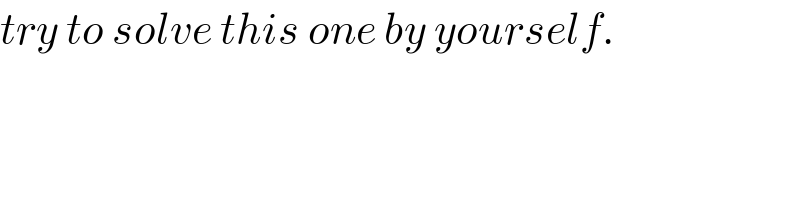
$${try}\:{to}\:{solve}\:{this}\:{one}\:{by}\:{yourself}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19

$$\mathrm{Ohh},\:\mathrm{good}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{will}\:\mathrm{try}\:\mathrm{it}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19
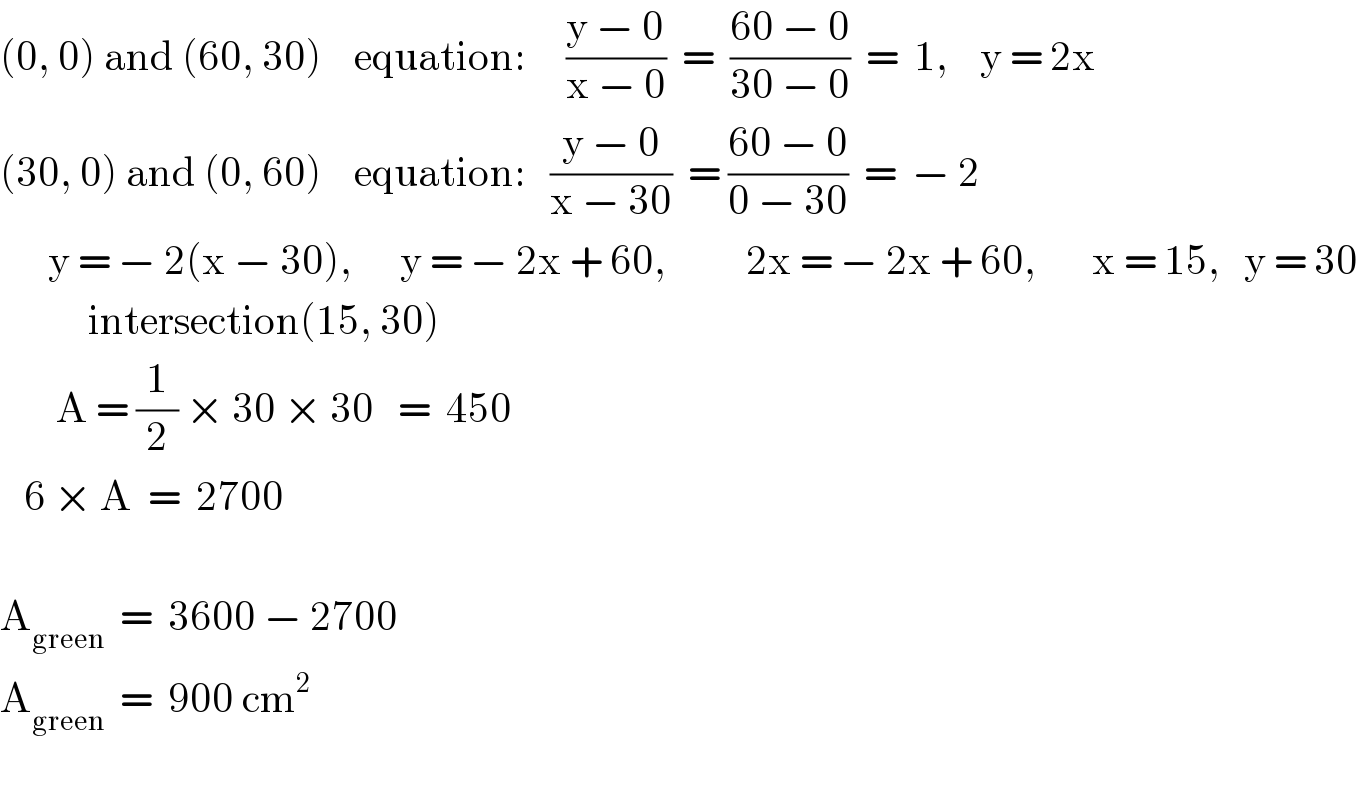
$$\left(\mathrm{0},\:\mathrm{0}\right)\:\mathrm{and}\:\left(\mathrm{60},\:\mathrm{30}\right)\:\:\:\:\mathrm{equation}:\:\:\:\:\:\frac{\mathrm{y}\:−\:\mathrm{0}}{\mathrm{x}\:−\:\mathrm{0}}\:\:=\:\:\frac{\mathrm{60}\:−\:\mathrm{0}}{\mathrm{30}\:−\:\mathrm{0}}\:\:=\:\:\mathrm{1},\:\:\:\:\mathrm{y}\:=\:\mathrm{2x} \\ $$$$\left(\mathrm{30},\:\mathrm{0}\right)\:\mathrm{and}\:\left(\mathrm{0},\:\mathrm{60}\right)\:\:\:\:\mathrm{equation}:\:\:\:\frac{\mathrm{y}\:−\:\mathrm{0}}{\mathrm{x}\:−\:\mathrm{30}}\:\:=\:\frac{\mathrm{60}\:−\:\mathrm{0}}{\mathrm{0}\:−\:\mathrm{30}}\:\:=\:\:−\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{y}\:=\:−\:\mathrm{2}\left(\mathrm{x}\:−\:\mathrm{30}\right),\:\:\:\:\:\:\mathrm{y}\:=\:−\:\mathrm{2x}\:+\:\mathrm{60},\:\:\:\:\:\:\:\:\:\:\mathrm{2x}\:=\:−\:\mathrm{2x}\:+\:\mathrm{60},\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{15},\:\:\:\mathrm{y}\:=\:\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{intersection}\left(\mathrm{15},\:\mathrm{30}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{A}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:×\:\mathrm{30}\:×\:\mathrm{30}\:\:\:=\:\:\mathrm{450} \\ $$$$\:\:\:\mathrm{6}\:×\:\mathrm{A}\:\:=\:\:\mathrm{2700} \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{green}} \:\:=\:\:\mathrm{3600}\:−\:\mathrm{2700} \\ $$$$\mathrm{A}_{\mathrm{green}} \:\:=\:\:\mathrm{900}\:\mathrm{cm}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by mr W last updated on 23/Aug/19
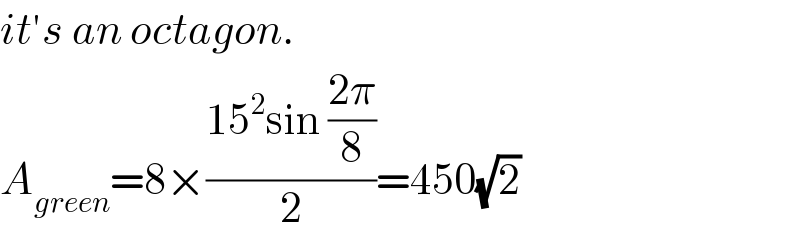
$${it}'{s}\:{an}\:{octagon}. \\ $$$${A}_{{green}} =\mathrm{8}×\frac{\mathrm{15}^{\mathrm{2}} \mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{8}}}{\mathrm{2}}=\mathrm{450}\sqrt{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
$$\mathrm{Haa},\:\mathrm{this}\:\mathrm{one}\:\mathrm{is}\:\mathrm{another}\:\mathrm{one}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19
$$\mathrm{Please}\:\mathrm{sir}\:\mathrm{teach}\:\mathrm{me}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19

$$\mathrm{I}\:\mathrm{only}\:\mathrm{used}\:\mathrm{the}\:\mathrm{approach}\:\mathrm{of}\:\mathrm{geometry}\:\mathrm{you}\:\mathrm{used}.\: \\ $$$$\mathrm{and}\:\mathrm{i}\:\mathrm{got}\:\mathrm{it}\:\mathrm{wrong}.\:\:\left(\smile\:.\:.\:\smile\right) \\ $$
Commented by Rasheed.Sindhi last updated on 24/Aug/19

$$\boldsymbol{\mathrm{S}}\mathrm{ir}\:\mathrm{is}\:\mathrm{it}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{octagon}?\:\mathrm{If}\:\mathrm{it}\:\mathrm{is}\:\mathrm{then}\:\mathrm{all}\:\mathrm{its} \\ $$$$\mathrm{vertices}\:\mathrm{must}\:\mathrm{be}\:\mathrm{concentric}.\mathrm{But}\:\mathrm{a}\:\mathrm{picture} \\ $$$$\mathrm{by}\:\mathrm{GeoGebra}\:\mathrm{raises}\:\mathrm{doubt}.\mathrm{S}{ee}\:{the} \\ $$$${following}\:{picture}.\:\mathrm{I}\:\mathrm{think}\:\mathrm{you}'\mathrm{ve}\:\mathrm{used} \\ $$$$\mathrm{the}\:\mathrm{formula}\:\mathrm{of}\:\mathrm{regular}\:\mathrm{octagon}\:\mathrm{for}\:\mathrm{area}. \\ $$
Commented by Rasheed.Sindhi last updated on 24/Aug/19
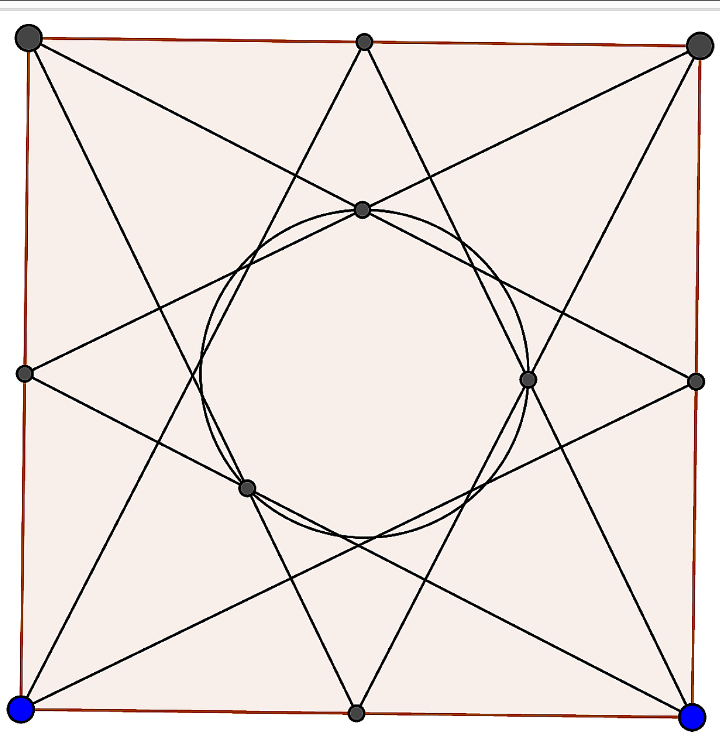
Commented by mr W last updated on 24/Aug/19
$${you}\:{are}\:{right}\:{sir}! \\ $$$${it}'{s}\:{slightly}\:{different}\:{from}\:{a} \\ $$$${regular}\:{octagon}. \\ $$$${the}\:{distance}\:{from}\:{its}\:{vertexes}\:{to} \\ $$$${its}\:{center}\:{is}\:\mathrm{15}\:{or}\:\mathrm{10}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{A}_{{green}} =\mathrm{8}×\frac{\mathrm{15}×\mathrm{10}\sqrt{\mathrm{2}}}{\mathrm{2}}×\mathrm{sin}\:\frac{\pi}{\mathrm{4}}=\mathrm{600} \\ $$
Commented by mr W last updated on 24/Aug/19

Commented by TawaTawa last updated on 24/Aug/19
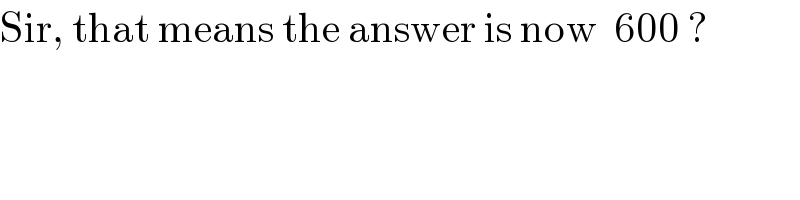
$$\mathrm{Sir},\:\mathrm{that}\:\mathrm{means}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{now}\:\:\mathrm{600}\:? \\ $$
Commented by mr W last updated on 24/Aug/19

$$\mathrm{600}\:{cm}^{\mathrm{2}} \:{is}\:{correct}. \\ $$
Commented by TawaTawa last updated on 24/Aug/19
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
