Menu Close

Question-67116

Tinku Tara 0 Comments
Pin




Question Number 67116 by TawaTawa last updated on 23/Aug/19
Commented by TawaTawa last updated on 23/Aug/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Kunal12588 last updated on 23/Aug/19
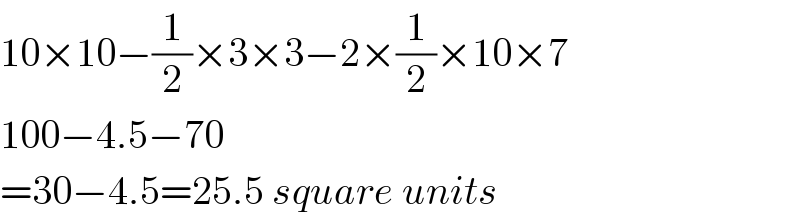
10×10−(1/2)×3×3−2×(1/2)×10×7 100−4.5−70 =30−4.5=25.5 square units
$$\mathrm{10}×\mathrm{10}−\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}×\mathrm{3}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{10}×\mathrm{7} \\ $$$$\mathrm{100}−\mathrm{4}.\mathrm{5}−\mathrm{70} \\ $$$$=\mathrm{30}−\mathrm{4}.\mathrm{5}=\mathrm{25}.\mathrm{5}\:{square}\:{units} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
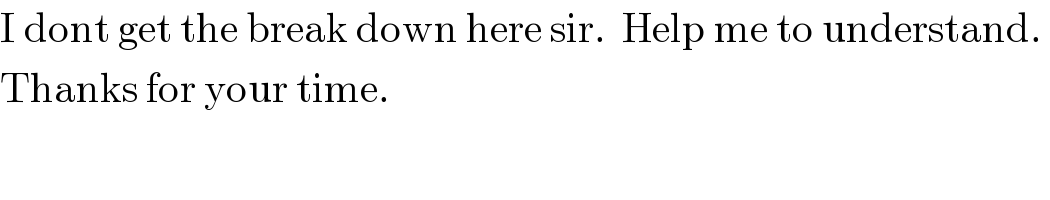
I dont get the break down here sir. Help me to understand. Thanks for your time.
$$\mathrm{I}\:\mathrm{dont}\:\mathrm{get}\:\mathrm{the}\:\mathrm{break}\:\mathrm{down}\:\mathrm{here}\:\mathrm{sir}.\:\:\mathrm{Help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{understand}.\: \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$
Answered by Kunal12588 last updated on 23/Aug/19
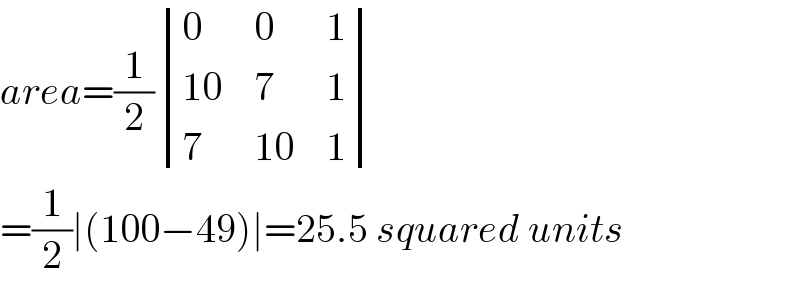
area=(1/2) determinant ((0,0,1),((10),7,1),(7,(10),1)) =(1/2)∣(100−49)∣=25.5 squared units
$${area}=\frac{\mathrm{1}}{\mathrm{2}}\begin{vmatrix}{\mathrm{0}}&{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{10}}&{\mathrm{7}}&{\mathrm{1}}\\{\mathrm{7}}&{\mathrm{10}}&{\mathrm{1}}\end{vmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\left(\mathrm{100}−\mathrm{49}\right)\mid=\mathrm{25}.\mathrm{5}\:{squared}\:{units} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
I appreciate sir
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 23/Aug/19
(1/2)×3(√2)×(10(√2)−(3/( (√2)))) =(1/2)×3(20−3) =((51)/2) =25.5
$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}\sqrt{\mathrm{2}}×\left(\mathrm{10}\sqrt{\mathrm{2}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}\left(\mathrm{20}−\mathrm{3}\right) \\ $$$$=\frac{\mathrm{51}}{\mathrm{2}} \\ $$$$=\mathrm{25}.\mathrm{5} \\ $$
Commented by mr W last updated on 23/Aug/19
Commented by TawaTawa last updated on 23/Aug/19
God bless you sir. Please let me see how you get 3(√2) (10(√2) − (3/( (√2)))) in the diagram. I am learning your approaches. Thanks for your time sir.
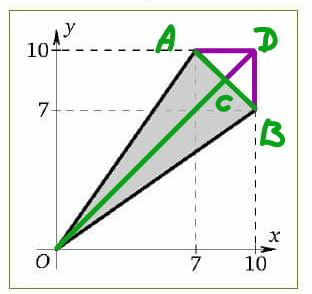
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{Please}\:\mathrm{let}\:\mathrm{me}\:\mathrm{see}\:\mathrm{how}\:\mathrm{you}\:\mathrm{get}\:\:\mathrm{3}\sqrt{\mathrm{2}}\:\left(\mathrm{10}\sqrt{\mathrm{2}}\:−\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{diagram}.\:\:\:\mathrm{I}\:\mathrm{am}\:\mathrm{learning}\:\mathrm{your}\:\mathrm{approaches}.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 23/Aug/19
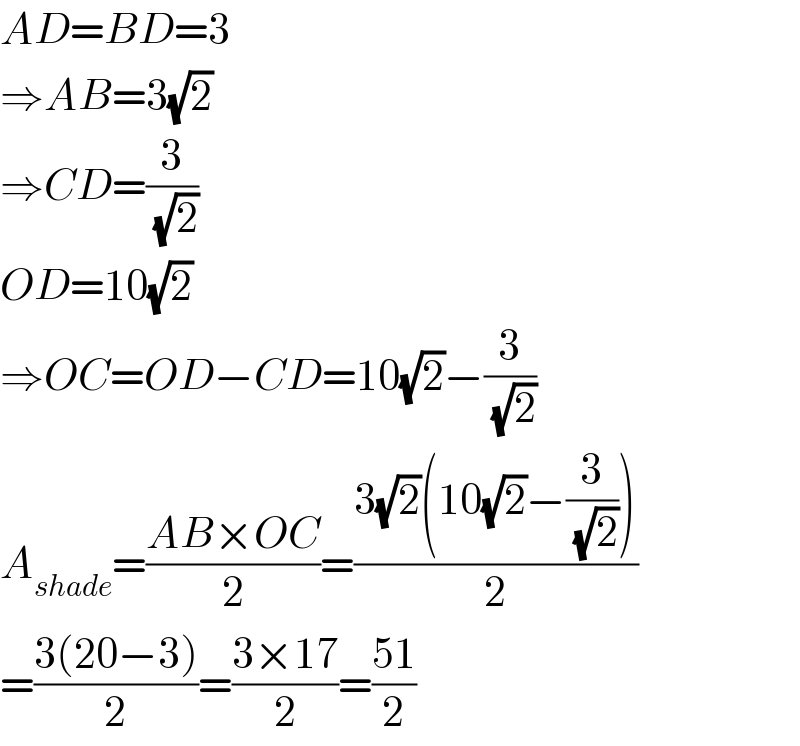
AD=BD=3 ⇒AB=3(√2) ⇒CD=(3/( (√2))) OD=10(√2) ⇒OC=OD−CD=10(√2)−(3/( (√2))) A_(shade) =((AB×OC)/2)=((3(√2)(10(√2)−(3/( (√2)))))/2) =((3(20−3))/2)=((3×17)/2)=((51)/2)
$${AD}={BD}=\mathrm{3} \\ $$$$\Rightarrow{AB}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{CD}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$$${OD}=\mathrm{10}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{OC}={OD}−{CD}=\mathrm{10}\sqrt{\mathrm{2}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$$${A}_{{shade}} =\frac{{AB}×{OC}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}\left(\mathrm{10}\sqrt{\mathrm{2}}−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}\left(\mathrm{20}−\mathrm{3}\right)}{\mathrm{2}}=\frac{\mathrm{3}×\mathrm{17}}{\mathrm{2}}=\frac{\mathrm{51}}{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
Wow, great, i understand sir.
$$\mathrm{Wow},\:\mathrm{great},\:\:\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19
Thanks for your time sir
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
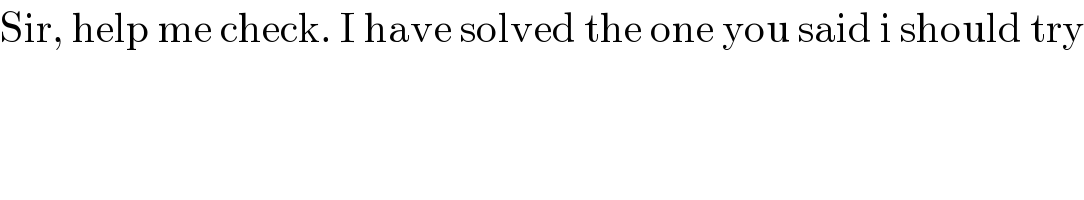
Sir, help me check. I have solved the one you said i should try
$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{check}.\:\mathrm{I}\:\mathrm{have}\:\mathrm{solved}\:\mathrm{the}\:\mathrm{one}\:\mathrm{you}\:\mathrm{said}\:\mathrm{i}\:\mathrm{should}\:\mathrm{try} \\ $$
Answered by Kunal12588 last updated on 23/Aug/19
question asks for easy way but lets try a hard way eq^n of line passing through O and (7,10) is y−0=((y−10)/(x−7))(x−0) ⇒y=((10)/7)x eq^n of line passing through O and (10,7) is y−0=((y−7)/(x−10))(x−0) ⇒y=(7/(10))x eq^n of line passing through (7,10) and (10,7) y−10=((y−7)/(x−10))(x−7) ⇒xy−10x−10y+100=xy−7x−7y+49 ⇒x+y=17 ⇒y=17−x area = ∫_0 ^7 ((10)/7)x dx + ∫_7 ^(10) (17−x)dx −∫_0 ^(10) (7/(10))x dx =((10)/7)×((49)/2)+17(10−7)−(((100)/2)−((49)/2))−(7/(10))×((100)/2) =35+51−((51)/2)−35 =((51)/2)=25.5
$${question}\:{asks}\:{for}\:{easy}\:{way}\:{but}\:{lets}\:{try}\:{a}\:{hard}\:{way} \\ $$$${eq}^{{n}} \:{of}\:{line}\:{passing}\:{through}\:{O}\:{and}\:\left(\mathrm{7},\mathrm{10}\right) \\ $$$${is}\:{y}−\mathrm{0}=\frac{{y}−\mathrm{10}}{{x}−\mathrm{7}}\left({x}−\mathrm{0}\right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{10}}{\mathrm{7}}{x} \\ $$$${eq}^{{n}} \:{of}\:{line}\:{passing}\:{through}\:{O}\:{and}\:\left(\mathrm{10},\mathrm{7}\right) \\ $$$${is}\:{y}−\mathrm{0}=\frac{{y}−\mathrm{7}}{{x}−\mathrm{10}}\left({x}−\mathrm{0}\right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{7}}{\mathrm{10}}{x} \\ $$$${eq}^{{n}} \:{of}\:{line}\:{passing}\:{through}\:\left(\mathrm{7},\mathrm{10}\right)\:{and}\:\left(\mathrm{10},\mathrm{7}\right) \\ $$$${y}−\mathrm{10}=\frac{{y}−\mathrm{7}}{{x}−\mathrm{10}}\left({x}−\mathrm{7}\right) \\ $$$$\Rightarrow{xy}−\mathrm{10}{x}−\mathrm{10}{y}+\mathrm{100}={xy}−\mathrm{7}{x}−\mathrm{7}{y}+\mathrm{49} \\ $$$$\Rightarrow{x}+{y}=\mathrm{17} \\ $$$$\Rightarrow{y}=\mathrm{17}−{x} \\ $$$${area}\:=\:\int_{\mathrm{0}} ^{\mathrm{7}} \:\frac{\mathrm{10}}{\mathrm{7}}{x}\:{dx}\:+\:\int_{\mathrm{7}} ^{\mathrm{10}} \left(\mathrm{17}−{x}\right){dx}\:−\int_{\mathrm{0}} ^{\mathrm{10}} \:\frac{\mathrm{7}}{\mathrm{10}}{x}\:{dx}\: \\ $$$$=\frac{\mathrm{10}}{\mathrm{7}}×\frac{\mathrm{49}}{\mathrm{2}}+\mathrm{17}\left(\mathrm{10}−\mathrm{7}\right)−\left(\frac{\mathrm{100}}{\mathrm{2}}−\frac{\mathrm{49}}{\mathrm{2}}\right)−\frac{\mathrm{7}}{\mathrm{10}}×\frac{\mathrm{100}}{\mathrm{2}} \\ $$$$=\mathrm{35}+\mathrm{51}−\frac{\mathrm{51}}{\mathrm{2}}−\mathrm{35} \\ $$$$=\frac{\mathrm{51}}{\mathrm{2}}=\mathrm{25}.\mathrm{5} \\ $$
Commented by TawaTawa last updated on 23/Aug/19
Wow, great sir. God bless you sir.
$$\mathrm{Wow},\:\mathrm{great}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 23/Aug/19
But sir, how do i choose area using integration
$$\mathrm{But}\:\mathrm{sir},\:\mathrm{how}\:\mathrm{do}\:\mathrm{i}\:\mathrm{choose}\:\mathrm{area}\:\mathrm{using}\:\mathrm{integration} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *