Question Number 147 by novrya last updated on 25/Jan/15
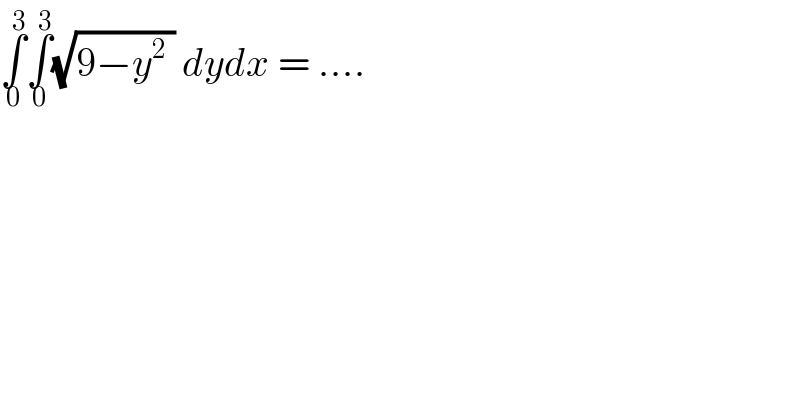
$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\sqrt{\mathrm{9}−{y}^{\mathrm{2}} \:}\:{dydx}\:=\:…. \\ $$
Answered by vkulkarni last updated on 11/Dec/14
![∫(√(a^2 −x^2 ))dx=(x/2)sin^(−1) (x/a)+(a^2 /2)(√(a^2 −x^2 ))+C This can be seen by putting x=asin θ ∫_0 ^3 ∫_0 ^3 (√(9−y^2 ))dydx=∫_0 ^3 [(y/2)sin^(−1) (y/3)+(9/2)(√(9−y^2 ))]_0 ^3 dx ∫_0 ^3 [(3/2)sin^(−1) (1)−((27)/2)]dx=3∙[(3/2)sin^(−1) (1)−((27)/2)]](https://www.tinkutara.com/question/Q148.png)
$$\int\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{{x}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{{a}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }+{C} \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{seen}\:\mathrm{by}\:\mathrm{putting}\:{x}={a}\mathrm{sin}\:\theta \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{9}−{y}^{\mathrm{2}} }{dydx}=\int_{\mathrm{0}} ^{\mathrm{3}} \left[\frac{{y}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \frac{{y}}{\mathrm{3}}+\frac{\mathrm{9}}{\mathrm{2}}\sqrt{\mathrm{9}−{y}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{3}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{3}} \left[\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}\right)−\frac{\mathrm{27}}{\mathrm{2}}\right]{dx}=\mathrm{3}\centerdot\left[\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}\right)−\frac{\mathrm{27}}{\mathrm{2}}\right] \\ $$
