Question Number 18797 by Tinkutara last updated on 29/Jul/17
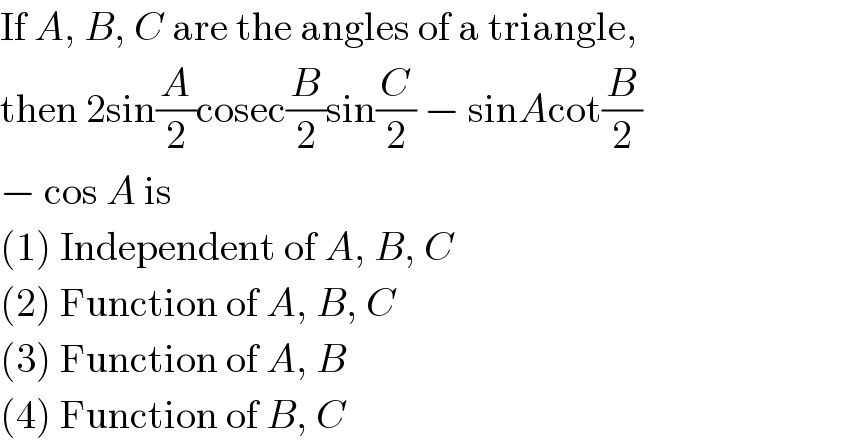
$$\mathrm{If}\:{A},\:{B},\:{C}\:\mathrm{are}\:\mathrm{the}\:\mathrm{angles}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}, \\ $$$$\mathrm{then}\:\mathrm{2sin}\frac{{A}}{\mathrm{2}}\mathrm{cosec}\frac{{B}}{\mathrm{2}}\mathrm{sin}\frac{{C}}{\mathrm{2}}\:−\:\mathrm{sin}{A}\mathrm{cot}\frac{{B}}{\mathrm{2}} \\ $$$$−\:\mathrm{cos}\:{A}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Independent}\:\mathrm{of}\:{A},\:{B},\:{C} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Function}\:\mathrm{of}\:{A},\:{B},\:{C} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Function}\:\mathrm{of}\:{A},\:{B} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{Function}\:\mathrm{of}\:{B},\:{C} \\ $$
Answered by behi.8.3.4.1.7@gmail.com last updated on 30/Jul/17

$$\frac{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}.{sin}\frac{{C}}{\mathrm{2}}}{{sin}\frac{{B}}{\mathrm{2}}}−\frac{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}}{{sin}\frac{{B}}{\mathrm{2}}}−{cosA}= \\ $$$$=\frac{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}\left({sin}\frac{{C}}{\mathrm{2}}−{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}\right)}{{sin}\frac{{B}}{\mathrm{2}}}−{cosA}= \\ $$$$−\mathrm{2}{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}−\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}\right)=−\mathrm{1}\:.\blacksquare \\ $$$$\Rightarrow{answer}\:\left(\mathrm{1}\right). \\ $$$${note}:{sin}\frac{{C}}{\mathrm{2}}={sin}\left(\mathrm{90}−\frac{{A}+{B}}{\mathrm{2}}\right)={cos}\frac{{A}+{B}}{\mathrm{2}}. \\ $$
Commented by Tinkutara last updated on 30/Jul/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{behi}\:\mathrm{Sir}! \\ $$
