Question Number 149 by rajabhay last updated on 25/Jan/15

$$\mathrm{if}\:\mathrm{tan}\:\mathrm{A}=\sqrt{\mathrm{2}}−\mathrm{1}\:\mathrm{then}\:\mathrm{find} \\ $$$$\frac{\mathrm{tan}\:\mathrm{A}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{A}}\:=\:? \\ $$
Answered by prakash jain last updated on 12/Dec/14
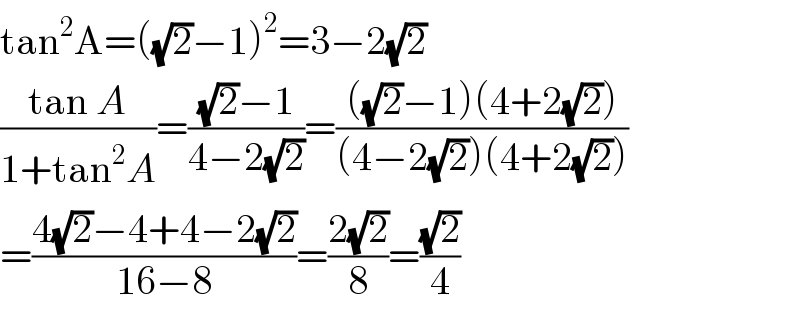
$$\mathrm{tan}^{\mathrm{2}} \mathrm{A}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{tan}\:{A}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {A}}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}=\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)}{\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{4}+\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{16}−\mathrm{8}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{8}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
