Question Number 1613 by 112358 last updated on 26/Aug/15
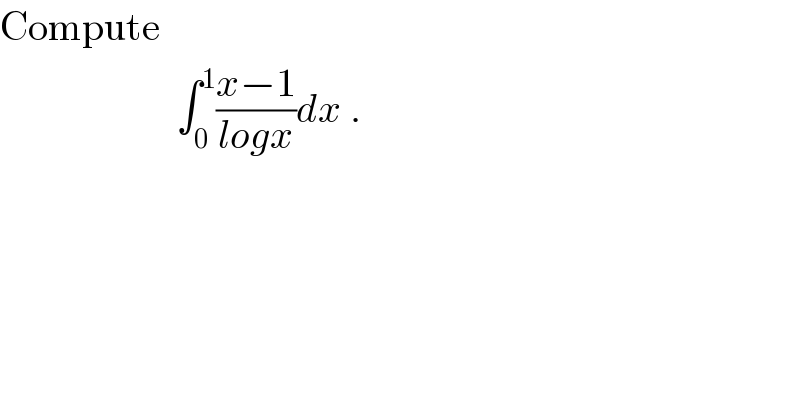
$$\mathrm{Compute}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{logx}}{dx}\:. \\ $$
Commented by 123456 last updated on 27/Aug/15
![I=ln 10 ln 2 j(x)=ln 10[Ei(2ln x)−li(x)]+C](https://www.tinkutara.com/question/Q1618.png)
$$\mathrm{I}=\mathrm{ln}\:\mathrm{10}\:\mathrm{ln}\:\mathrm{2} \\ $$$${j}\left({x}\right)=\mathrm{ln}\:\mathrm{10}\left[\mathrm{Ei}\left(\mathrm{2ln}\:{x}\right)−\mathrm{li}\left({x}\right)\right]+\mathrm{C} \\ $$
