If-the-equation-sin6x-cos4x-2-have-a-family-of-nonnegative-solutions-x-k-s-where-0-x-1-lt-x-2-lt-x-3-lt-lt-x-k-lt-x-k-1-then-the-value-of-1-pi-k-1-1000-x-

Question Number 18892 by Tinkutara last updated on 01/Aug/17

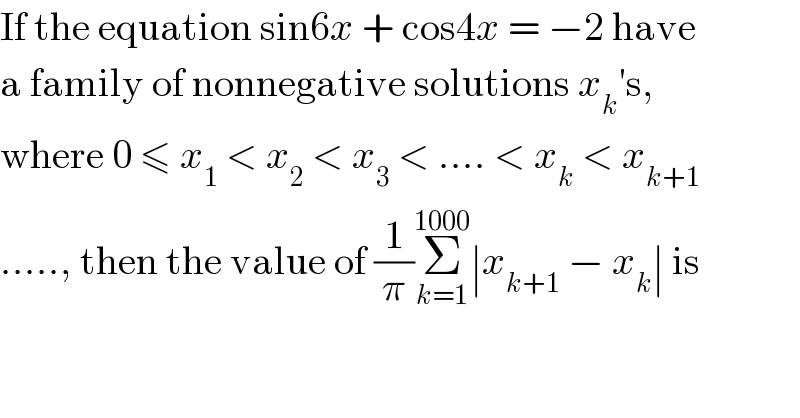
If the equation sin6x + cos4x = −2 have a family of nonnegative solutions x_k ′s, where 0 ≤ x_1 < x_2 < x_3 < .... < x_k < x_(k+1) ....., then the value of (1/π)Σ_(k=1) ^(1000) ∣x_(k+1) − x_k ∣ is

$$\mathrm{If}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{sin6}{x}\:+\:\mathrm{cos4}{x}\:=\:−\mathrm{2}\:\mathrm{have} \\ $$$$\mathrm{a}\:\mathrm{family}\:\mathrm{of}\:\mathrm{nonnegative}\:\mathrm{solutions}\:{x}_{{k}} '\mathrm{s}, \\ $$$$\mathrm{where}\:\mathrm{0}\:\leqslant\:{x}_{\mathrm{1}} \:<\:{x}_{\mathrm{2}} \:<\:{x}_{\mathrm{3}} \:<\:….\:<\:{x}_{{k}} \:<\:{x}_{{k}+\mathrm{1}} \\ $$$$…..,\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{1}}{\pi}\underset{{k}=\mathrm{1}} {\overset{\mathrm{1000}} {\sum}}\mid{x}_{{k}+\mathrm{1}} \:−\:{x}_{{k}} \mid\:\mathrm{is} \\ $$

Answered by ajfour last updated on 01/Aug/17

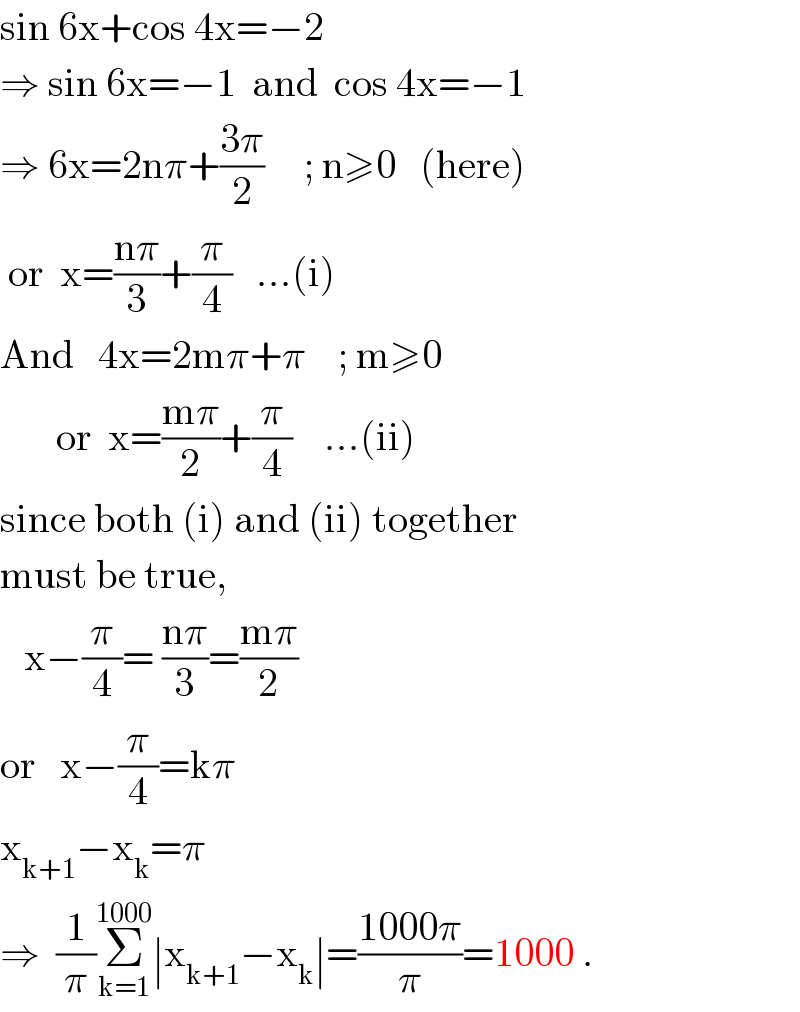
sin 6x+cos 4x=−2 ⇒ sin 6x=−1 and cos 4x=−1 ⇒ 6x=2nπ+((3π)/2) ; n≥0 (here) or x=((nπ)/3)+(π/4) ...(i) And 4x=2mπ+π ; m≥0 or x=((mπ)/2)+(π/4) ...(ii) since both (i) and (ii) together must be true, x−(π/4)= ((nπ)/3)=((mπ)/2) or x−(π/4)=kπ x_(k+1) −x_k =π ⇒ (1/π)Σ_(k=1) ^(1000) ∣x_(k+1) −x_k ∣=((1000π)/π)=1000 .

$$\mathrm{sin}\:\mathrm{6x}+\mathrm{cos}\:\mathrm{4x}=−\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{6x}=−\mathrm{1}\:\:\mathrm{and}\:\:\mathrm{cos}\:\mathrm{4x}=−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{6x}=\mathrm{2n}\pi+\frac{\mathrm{3}\pi}{\mathrm{2}}\:\:\:\:\:;\:\mathrm{n}\geqslant\mathrm{0}\:\:\:\left(\mathrm{here}\right) \\ $$$$\:\mathrm{or}\:\:\mathrm{x}=\frac{\mathrm{n}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{4}}\:\:\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{And}\:\:\:\mathrm{4x}=\mathrm{2m}\pi+\pi\:\:\:\:;\:\mathrm{m}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{or}\:\:\mathrm{x}=\frac{\mathrm{m}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$$\mathrm{since}\:\mathrm{both}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\:\mathrm{together} \\ $$$$\mathrm{must}\:\mathrm{be}\:\mathrm{true}, \\ $$$$\:\:\:\mathrm{x}−\frac{\pi}{\mathrm{4}}=\:\frac{\mathrm{n}\pi}{\mathrm{3}}=\frac{\mathrm{m}\pi}{\mathrm{2}} \\ $$$$\mathrm{or}\:\:\:\mathrm{x}−\frac{\pi}{\mathrm{4}}=\mathrm{k}\pi\:\: \\ $$$$\mathrm{x}_{\mathrm{k}+\mathrm{1}} −\mathrm{x}_{\mathrm{k}} =\pi \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\pi}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{1000}} {\sum}}\mid\mathrm{x}_{\mathrm{k}+\mathrm{1}} −\mathrm{x}_{\mathrm{k}} \mid=\frac{\mathrm{1000}\pi}{\pi}=\mathrm{1000}\:. \\ $$

Commented by ajfour last updated on 01/Aug/17

$$\mathrm{is}\:\mathrm{it}\:\mathrm{correct}? \\ $$

Commented by Tinkutara last updated on 01/Aug/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{ajfour}\:\mathrm{Sir}! \\ $$

Facebook Tweet Pin

If-the-equation-sin6x-cos4x-2-have-a-family-of-nonnegative-solutions-x-k-s-where-0-x-1-lt-x-2-lt-x-3-lt-lt-x-k-lt-x-k-1-then-the-value-of-1-pi-k-1-1000-x-

Leave a Reply Cancel reply