Question Number 67167 by behi83417@gmail.com last updated on 23/Aug/19
![solve for real x and y:[a,b∈R] a. { ((x^3 +1=y^3 )),((x^2 +1=y^2 )) :} b. { ((x^3 +x^2 +1=y^3 )),((x^2 +x+1=y^2 )) :} c. { ((x^3 +y^2 =9xy)),((x^2 +y^3 =8xy)) :} d. { ((ax+by=2ab)),((x^2 +y^2 =4abxy)) :}](https://www.tinkutara.com/question/Q67167.png)
$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{real}}\:\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{and}}\:\:\boldsymbol{\mathrm{y}}:\left[\mathrm{a},\mathrm{b}\in\mathrm{R}\right] \\ $$$$\boldsymbol{\mathrm{a}}.\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{3}} }\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\end{cases}\:\:\:\:\:\:\:\: \\ $$$$\boldsymbol{\mathrm{b}}.\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{3}} }\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\end{cases} \\ $$$$\boldsymbol{\mathrm{c}}.\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{9}\boldsymbol{\mathrm{xy}}}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{3}} =\mathrm{8}\boldsymbol{\mathrm{xy}}}\end{cases} \\ $$$$\boldsymbol{\mathrm{d}}.\begin{cases}{\boldsymbol{\mathrm{ax}}+\boldsymbol{\mathrm{by}}=\mathrm{2}\boldsymbol{\mathrm{ab}}}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{4}\boldsymbol{\mathrm{abxy}}}\end{cases} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Aug/19
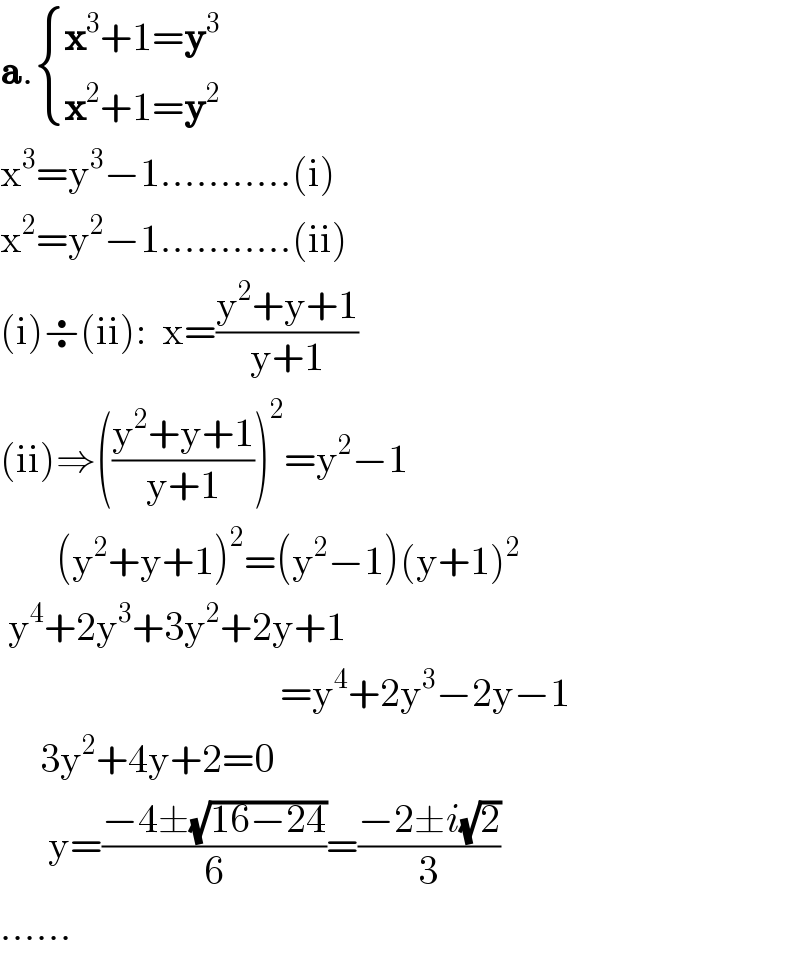
$$\boldsymbol{\mathrm{a}}.\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{3}} }\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} }\end{cases}\:\:\:\:\:\:\:\: \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{y}^{\mathrm{3}} −\mathrm{1}………..\left(\mathrm{i}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{y}^{\mathrm{2}} −\mathrm{1}………..\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\boldsymbol{\div}\left(\mathrm{ii}\right):\:\:\mathrm{x}=\frac{\mathrm{y}^{\mathrm{2}} +\mathrm{y}+\mathrm{1}}{\mathrm{y}+\mathrm{1}} \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\left(\frac{\mathrm{y}^{\mathrm{2}} +\mathrm{y}+\mathrm{1}}{\mathrm{y}+\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{y}^{\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{y}^{\mathrm{2}} +\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{y}^{\mathrm{4}} +\mathrm{2y}^{\mathrm{3}} +\mathrm{3y}^{\mathrm{2}} +\mathrm{2y}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{y}^{\mathrm{4}} +\mathrm{2y}^{\mathrm{3}} −\mathrm{2y}−\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{3y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{y}=\frac{−\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{24}}}{\mathrm{6}}=\frac{−\mathrm{2}\pm{i}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$…… \\ $$
Commented by behi83417@gmail.com last updated on 23/Aug/19
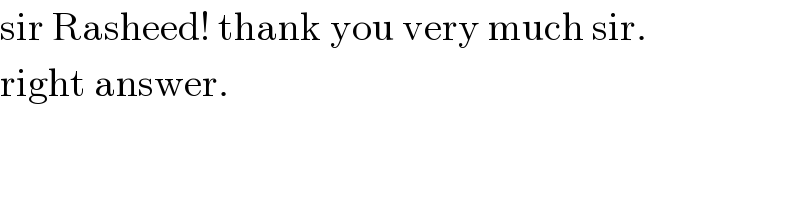
$$\mathrm{sir}\:\mathrm{Rasheed}!\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$$$\mathrm{right}\:\mathrm{answer}. \\ $$
Answered by MJS last updated on 23/Aug/19

$${a} \\ $$$${y}=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$${x}^{\mathrm{2}} +\mathrm{1}=\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} =\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{0}\wedge{y}=\mathrm{1} \\ $$$$ \\ $$$${b} \\ $$$${y}=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{3}} =\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{0}\wedge{y}=\mathrm{1} \\ $$$${x}=−\mathrm{1}\wedge{y}=\mathrm{1} \\ $$$${x}=−\frac{\mathrm{4}}{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{173}}{\mathrm{54}}−\frac{\sqrt{\mathrm{29}}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{173}}{\mathrm{54}}+\frac{\sqrt{\mathrm{29}}}{\mathrm{2}}}\wedge{y}=−\frac{\mathrm{5}}{\mathrm{3}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{61}}{\mathrm{54}}−\frac{\sqrt{\mathrm{29}}}{\mathrm{6}}}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{61}}{\mathrm{54}}+\frac{\sqrt{\mathrm{29}}}{\mathrm{6}}} \\ $$
Answered by MJS last updated on 23/Aug/19

$${c} \\ $$$${x}=\mathrm{0}\wedge{y}=\mathrm{0} \\ $$$$\mathrm{leading}\:\mathrm{to}\:\mathrm{polynomes}\:\mathrm{of}\:\mathrm{5}^{\mathrm{th}} \:\mathrm{degree} \\ $$$$\Rightarrow \\ $$$${x}\approx.\mathrm{0976275}\wedge{y}\approx.\mathrm{877587} \\ $$$${x}\approx\mathrm{1}.\mathrm{11177}\wedge{y}\approx.\mathrm{139274} \\ $$$${x}\approx\mathrm{7}.\mathrm{66375}\wedge{y}\approx\mathrm{7}.\mathrm{29810} \\ $$
Answered by MJS last updated on 23/Aug/19
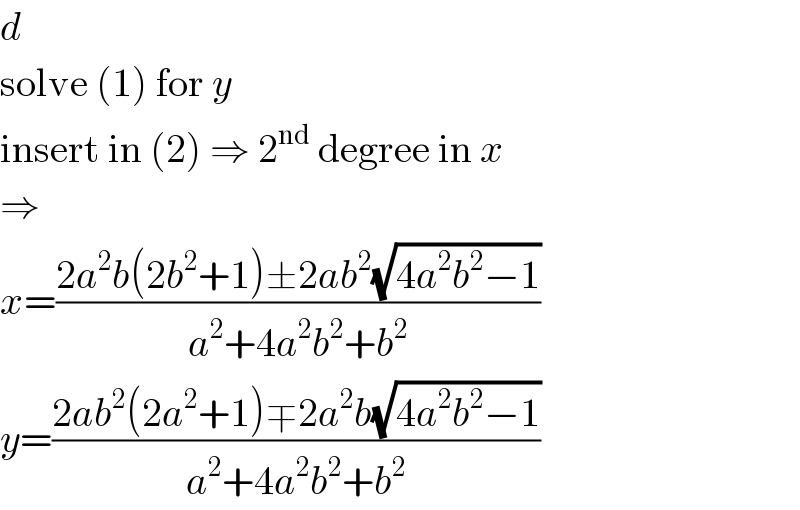
$${d} \\ $$$$\mathrm{solve}\:\left(\mathrm{1}\right)\:\mathrm{for}\:{y} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{degree}\:\mathrm{in}\:{x} \\ $$$$\Rightarrow \\ $$$${x}=\frac{\mathrm{2}{a}^{\mathrm{2}} {b}\left(\mathrm{2}{b}^{\mathrm{2}} +\mathrm{1}\right)\pm\mathrm{2}{ab}^{\mathrm{2}} \sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{1}}}{{a}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$${y}=\frac{\mathrm{2}{ab}^{\mathrm{2}} \left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{1}\right)\mp\mathrm{2}{a}^{\mathrm{2}} {b}\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{1}}}{{a}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$
Commented by behi83417@gmail.com last updated on 23/Aug/19

$$\mathrm{dear}\:\mathrm{proph}.\:\mathrm{MJS}!\:\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{sir}. \\ $$$$\mathrm{right}\:\mathrm{answers},\mathrm{smart}\:\mathrm{solutions},\mathrm{and}\: \\ $$$$\mathrm{beautiful}\:\mathrm{methods}. \\ $$$$\mathrm{your}\:\mathrm{answers}\:\mathrm{are},\mathrm{always}\:,\mathrm{the}\:\mathrm{final} \\ $$$$\mathrm{shoot}\:\mathrm{to}\:\mathrm{the}\:\mathrm{question}. \\ $$$$\mathrm{happy}\:\mathrm{and}\:\mathrm{thankful}\:\mathrm{for}\:\mathrm{being}\:\mathrm{you}\:\mathrm{in} \\ $$$$\mathrm{this}\:\mathrm{forum}\:\mathrm{sir}.\mathrm{god}\:\mathrm{bless}\:\mathrm{you}. \\ $$$$ \\ $$
Commented by MJS last updated on 23/Aug/19

$$\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{you}'\mathrm{re}\:\mathrm{always}\:\mathrm{welcome} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Aug/19
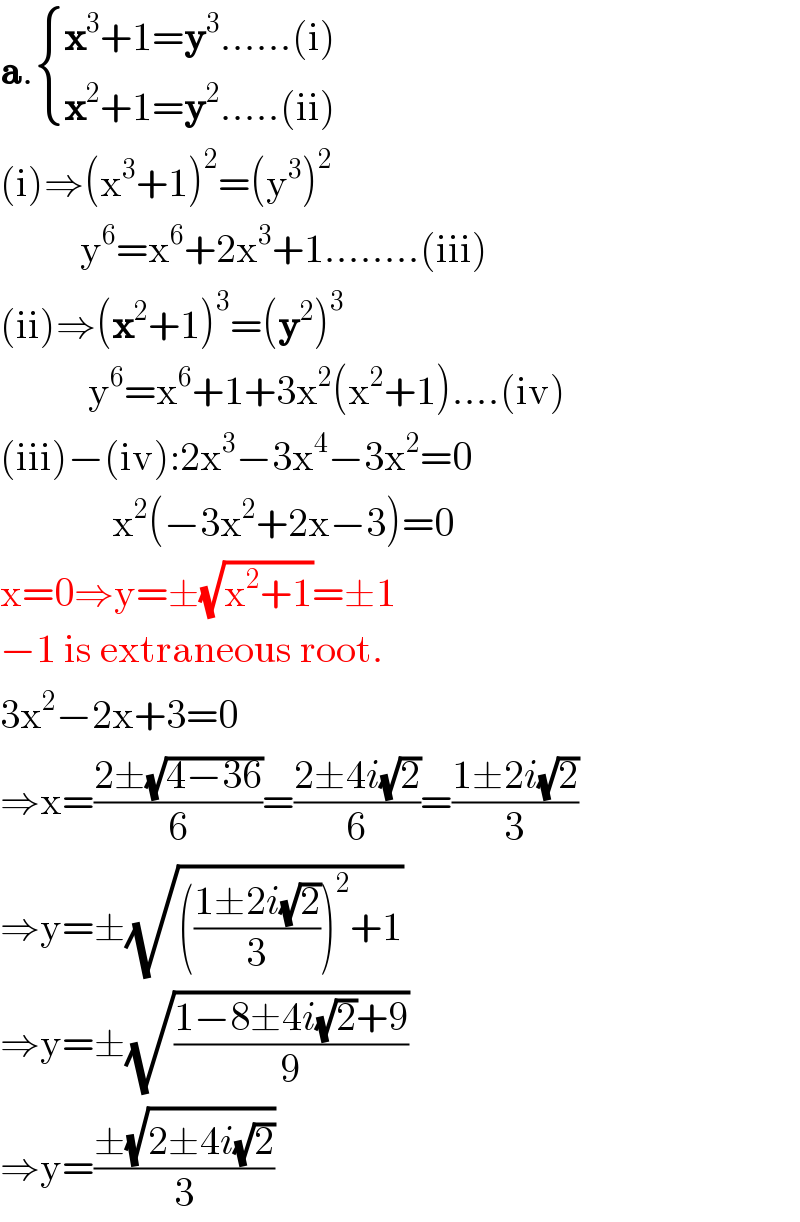
$$\boldsymbol{\mathrm{a}}.\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{3}} ……\left(\mathrm{i}\right)}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}=\boldsymbol{\mathrm{y}}^{\mathrm{2}} …..\left(\mathrm{ii}\right)}\end{cases}\:\:\:\:\:\:\:\: \\ $$$$\left(\mathrm{i}\right)\Rightarrow\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{y}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{6}} =\mathrm{x}^{\mathrm{6}} +\mathrm{2x}^{\mathrm{3}} +\mathrm{1}……..\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} =\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{6}} =\mathrm{x}^{\mathrm{6}} +\mathrm{1}+\mathrm{3x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)….\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iii}\right)−\left(\mathrm{iv}\right):\mathrm{2x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \left(−\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{x}=\mathrm{0}\Rightarrow\mathrm{y}=\pm\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\pm\mathrm{1} \\ $$$$−\mathrm{1}\:\mathrm{is}\:\mathrm{extraneous}\:\mathrm{root}. \\ $$$$\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{36}}}{\mathrm{6}}=\frac{\mathrm{2}\pm\mathrm{4}{i}\sqrt{\mathrm{2}}}{\mathrm{6}}=\frac{\mathrm{1}\pm\mathrm{2}{i}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{y}=\pm\sqrt{\left(\frac{\mathrm{1}\pm\mathrm{2}{i}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\mathrm{y}=\pm\sqrt{\frac{\mathrm{1}−\mathrm{8}\pm\mathrm{4}{i}\sqrt{\mathrm{2}}+\mathrm{9}}{\mathrm{9}}} \\ $$$$\Rightarrow\mathrm{y}=\frac{\pm\sqrt{\mathrm{2}\pm\mathrm{4}{i}\sqrt{\mathrm{2}}}}{\mathrm{3}} \\ $$
