Menu Close

dx-x-2-x-1-2-

Tinku Tara 0 Comments
Pin




Question Number 150079 by puissant last updated on 09/Aug/21
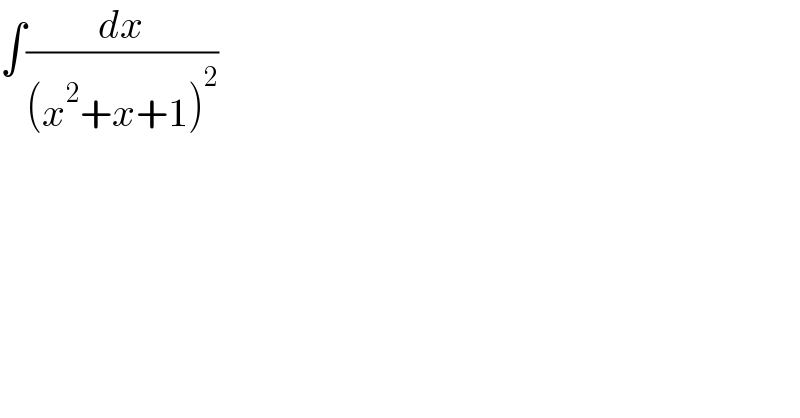
∫(dx/((x^2 +x+1)^2 ))
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 09/Aug/21
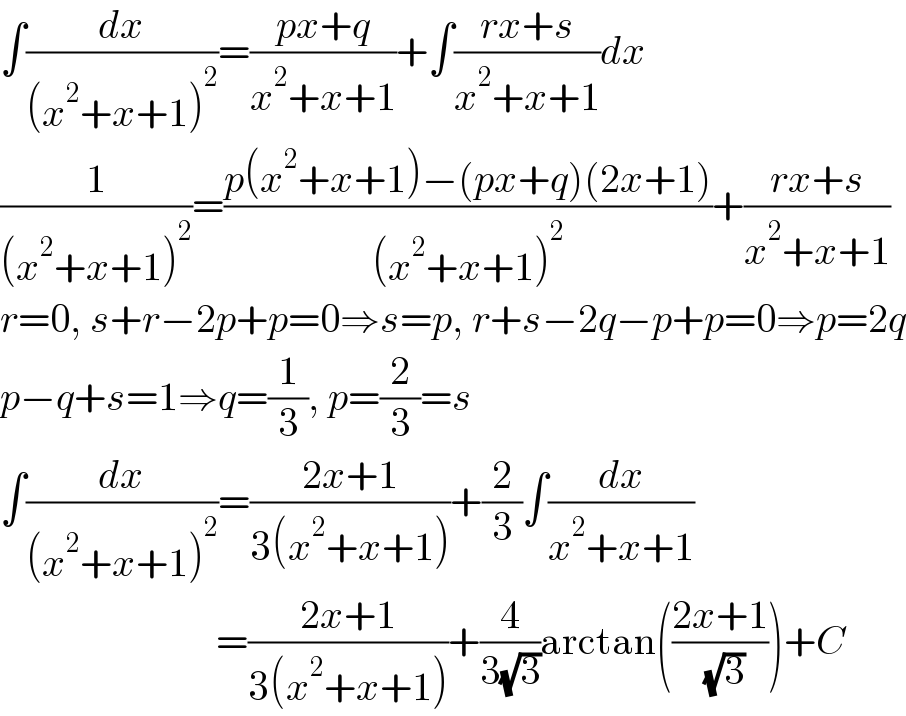
∫(dx/((x^2 +x+1)^2 ))=((px+q)/(x^2 +x+1))+∫((rx+s)/(x^2 +x+1))dx (1/((x^2 +x+1)^2 ))=((p(x^2 +x+1)−(px+q)(2x+1))/((x^2 +x+1)^2 ))+((rx+s)/(x^2 +x+1)) r=0, s+r−2p+p=0⇒s=p, r+s−2q−p+p=0⇒p=2q p−q+s=1⇒q=(1/3), p=(2/3)=s ∫(dx/((x^2 +x+1)^2 ))=((2x+1)/(3(x^2 +x+1)))+(2/3)∫(dx/(x^2 +x+1)) =((2x+1)/(3(x^2 +x+1)))+(4/(3(√3)))arctan(((2x+1)/( (√3))))+C
$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{px}+{q}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\int\frac{{rx}+{s}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{p}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)−\left({px}+{q}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{rx}+{s}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$${r}=\mathrm{0},\:{s}+{r}−\mathrm{2}{p}+{p}=\mathrm{0}\Rightarrow{s}={p},\:{r}+{s}−\mathrm{2}{q}−{p}+{p}=\mathrm{0}\Rightarrow{p}=\mathrm{2}{q} \\ $$$${p}−{q}+{s}=\mathrm{1}\Rightarrow{q}=\frac{\mathrm{1}}{\mathrm{3}},\:{p}=\frac{\mathrm{2}}{\mathrm{3}}={s} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$
Commented by puissant last updated on 09/Aug/21
propre merci bro..
$${propre}\:{merci}\:{bro}.. \\ $$
Commented by puissant last updated on 09/Aug/21
mais t′as oublie^� l′integrale au nivau de la premiere ligne broo
$${mais}\:{t}'{as}\:{oubli}\acute {{e}}\:{l}'{integrale}\:{au}\:{nivau} \\ $$$${de}\:{la}\:{premiere}\:{ligne}\:{broo} \\ $$
Commented by Ar Brandon last updated on 09/Aug/21
J′ai de^� rive^� l′e^� galite^� au niveau de la premie^� re ligne pour avoir celle sur la deuxie^� me.
$$\mathrm{J}'\mathrm{ai}\:\mathrm{d}\acute {\mathrm{e}riv}\acute {\mathrm{e}}\:\mathrm{l}'\acute {\mathrm{e}galit}\acute {\mathrm{e}}\:\mathrm{au}\:\mathrm{niveau}\:\mathrm{de}\:\mathrm{la}\:\mathrm{premi}\grave {\mathrm{e}re} \\ $$$$\:\mathrm{ligne}\:\mathrm{pour}\:\mathrm{avoir}\:\mathrm{celle}\:\mathrm{sur}\:\mathrm{la}\:\mathrm{deuxi}\grave {\mathrm{e}me}. \\ $$
Commented by puissant last updated on 09/Aug/21
je pensais que c′etait la decomposition en element simple..
$${je}\:{pensais}\:{que}\:{c}'{etait}\:{la}\:{decomposition} \\ $$$${en}\:{element}\:{simple}.. \\ $$
Commented by Ar Brandon last updated on 09/Aug/21
Il s′agit de la me^� thode d′Ostrogradsky que M. MJS m′avait appris; celui dont je t′avais parle^� lors de notre conversation sur whatsapp. 😊😇😃 METHODE D′OSTROGRADSKY Soit ∫((P(x))/(Q(x)))dx. D,ou^� P(x) et Q(x) sont des polyno^� mes avec deg(P(x))<deg(Q(x)) et ((P(x))/(Q(x))) irreductible alors ∫((P(x))/(Q(x)))dx=((P_1 (x))/(Q_1 (x)))+∫((P_2 (x))/(Q_2 (x)))dx D′ou^� Q_1 (x)=pgcd(Q(x); Q′(x)) et Q_2 (x)=((Q(x))/(Q_1 (x))) P_1 (x) et P_2 (x) sont des polyno^� mes a^� chercher.
$$\mathrm{Il}\:\mathrm{s}'\mathrm{agit}\:\mathrm{de}\:\mathrm{la}\:\mathrm{m}\acute {\mathrm{e}thode}\:\mathrm{d}'\mathrm{Ostrogradsky}\:\mathrm{que}\:\mathrm{M}.\:\mathrm{MJS}\:\mathrm{m}'\mathrm{avait} \\ $$$$\mathrm{appris};\:\mathrm{celui}\:\mathrm{dont}\:\mathrm{je}\:\mathrm{t}'\mathrm{avais}\:\mathrm{parl}\acute {\mathrm{e}}\:\mathrm{lors}\:\mathrm{de}\:\mathrm{notre}\:\mathrm{conversation} \\ $$$$\mathrm{sur}\:\mathrm{whatsapp}.\: \\ $$😊😇😃
$$\mathcal{METHODE}\:\:\:\:\mathcal{D}'\mathcal{OSTROGRADSKY} \\ $$$$\mathrm{Soit}\:\int\frac{\mathrm{P}\left(\mathrm{x}\right)}{\mathrm{Q}\left(\mathrm{x}\right)}\mathrm{dx}.\:\mathrm{D},\mathrm{o}\grave {\mathrm{u}}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{et}\:\mathrm{Q}\left(\mathrm{x}\right)\:\mathrm{sont}\:\mathrm{des}\:\mathrm{polyn}\hat {\mathrm{o}mes}\:\mathrm{avec} \\ $$$$\mathrm{deg}\left(\mathrm{P}\left(\mathrm{x}\right)\right)<\mathrm{deg}\left(\mathrm{Q}\left(\mathrm{x}\right)\right)\:\mathrm{et}\:\frac{\mathrm{P}\left(\mathrm{x}\right)}{\mathrm{Q}\left(\mathrm{x}\right)}\:\mathrm{irreductible}\:\mathrm{alors} \\ $$$$\int\frac{\mathrm{P}\left(\mathrm{x}\right)}{\mathrm{Q}\left(\mathrm{x}\right)}\mathrm{dx}=\frac{\mathrm{P}_{\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{Q}_{\mathrm{1}} \left(\mathrm{x}\right)}+\int\frac{\mathrm{P}_{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{Q}_{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\mathrm{D}'\mathrm{o}\grave {\mathrm{u}}\:\mathrm{Q}_{\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{pgcd}\left(\mathrm{Q}\left(\mathrm{x}\right);\:\mathrm{Q}'\left(\mathrm{x}\right)\right)\:\mathrm{et}\:\mathrm{Q}_{\mathrm{2}} \left(\mathrm{x}\right)=\frac{\mathrm{Q}\left(\mathrm{x}\right)}{\mathrm{Q}_{\mathrm{1}} \left(\mathrm{x}\right)} \\ $$$$\mathrm{P}_{\mathrm{1}} \left(\mathrm{x}\right)\:\mathrm{et}\:\mathrm{P}_{\mathrm{2}} \left(\mathrm{x}\right)\:\mathrm{sont}\:\mathrm{des}\:\mathrm{polyn}\hat {\mathrm{o}mes}\:\grave {\mathrm{a}}\:\mathrm{chercher}. \\ $$
Commented by puissant last updated on 09/Aug/21
D′accord
$${D}'{accord}\: \\ $$
Answered by mathmax by abdo last updated on 09/Aug/21
let f(a)=∫ (dx/(x^2 +x+a))( a>(1/(4)))) ⇒f^′ (x)=−∫ (dx/((x^2 +x+a)^2 )) ⇒ f^′ (1)=−∫ (dx/((x^2 +x+1)^2 )) ⇒∫ (dx/((x^2 +x+1)^2 ))=−f^′ (1) f(a)=∫ (dx/(x^2 +2(x/2)x +(1/4)+a−(1/4)))=∫ (dx/((x+(1/2))^2 +((4a−1)/4))) =_(x+(1/2)=((√(4a−1))/2)u) ∫ (1/(((4a−1)/4)(1+u^2 )))×((√(4a−1))/2)du =(4/(4a−1))×((√(4a−1))/2) ∫ (du/(1+u^2 )) =(2/( (√(4a−1)))) arctan(((2x+1)/( (√(4a−1)))))+c ⇒ f^′ (a)=2(d/da)((4a−1)^(−(1/2)) arctan(((2x+1)/( (√(4a−1)))))) =2.(−(1/2))(4)(4a−1)^(−(3/2)) arctan(((2x+1)/( (√(4a−1))))) +2(4a−1)^(−(1/2)) .((2/( (√(4a−1))))/(1+(((2x+1)/( (√(4a−1)))))^2 )) =((−4)/((4a−1)(√(4a−1)))) arctan(((2x+1)/( (√(4a−1))))) +(4/((4a−1)(1+(((2x+1)/( (√(4a−1)))))^2 ))) f^′ (1)=((−4)/(3(√3))) arctan(((2x+1)/( (√3))))+(4/(3(1+(((2x+1)/( (√3))))^2 ))) ⇒ ∫ (dx/((x^2 +x+1)^2 ))=(4/(3(√3)))arctan(((2x+1)/( (√3))))−(4/(3(1+(1/3)(2x+1)^2 ))) +c
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}}\left(\:\mathrm{a}>\frac{\mathrm{1}}{\left.\mathrm{4}\right)}\right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=−\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{1}\right)=−\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{x}}{\mathrm{2}}\mathrm{x}\:+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{a}−\frac{\mathrm{1}}{\mathrm{4}}}=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}}} \\ $$$$=_{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{u}} \:\:\:\:\int\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{4a}−\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}×\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\mathrm{du} \\ $$$$=\frac{\mathrm{4}}{\mathrm{4a}−\mathrm{1}}×\frac{\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\mathrm{2}\frac{\mathrm{d}}{\mathrm{da}}\left(\left(\mathrm{4a}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\right) \\ $$$$=\mathrm{2}.\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{4}\right)\left(\mathrm{4a}−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right) \\ $$$$+\mathrm{2}\left(\mathrm{4a}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:.\frac{\frac{\mathrm{2}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}}{\mathrm{1}+\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{4}}{\left(\mathrm{4a}−\mathrm{1}\right)\sqrt{\mathrm{4a}−\mathrm{1}}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)\:+\frac{\mathrm{4}}{\left(\mathrm{4a}−\mathrm{1}\right)\left(\mathrm{1}+\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\right)^{\mathrm{2}} \right)} \\ $$$$\mathrm{f}^{'} \left(\mathrm{1}\right)=\frac{−\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\int\:\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} \right)}\:+\mathrm{c} \\ $$
Commented by puissant last updated on 10/Aug/21
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *