Menu Close

x-2-cos-px-q-x-2-p-q-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 132708 by frc2crc last updated on 16/Feb/21
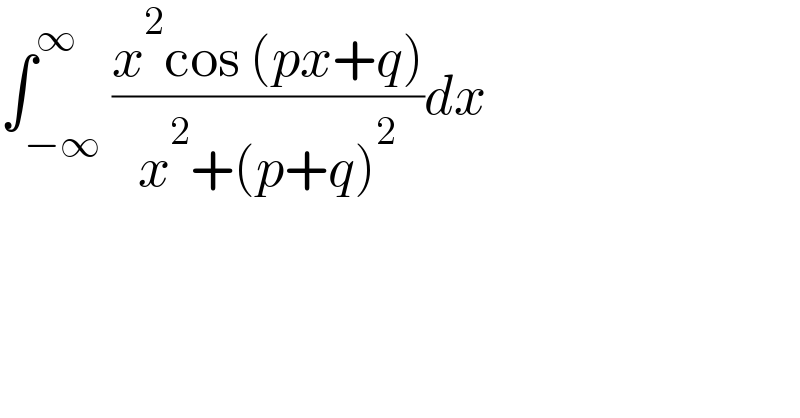
∫_(−∞) ^∞ ((x^2 cos (px+q))/(x^2 +(p+q)^2 ))dx
$$\int_{−\infty} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{cos}\:\left({px}+{q}\right)}{{x}^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by Olaf last updated on 16/Feb/21
Ω = ∫_(−∞) ^(+∞) ((x^2 cos(px+q))/(x^2 +(p+q)^2 ))dx Ω = ∫_(−∞) ^(+∞) ((x^2 [cos(px)cosq−sin(px)sinq])/(x^2 +(p+q)^2 ))dx Ω = cosq∫_(−∞) ^(+∞) ((x^2 cos(px))/(x^2 +(p+q)^2 ))dx ... now see Q.132090 by rs4090
$$ \\ $$$$\Omega\:=\:\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} \mathrm{cos}\left({px}+{q}\right)}{{x}^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} }{dx} \\ $$$$\Omega\:=\:\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} \left[\mathrm{cos}\left({px}\right)\mathrm{cos}{q}−\mathrm{sin}\left({px}\right)\mathrm{sin}{q}\right]}{{x}^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} }{dx} \\ $$$$\Omega\:=\:\mathrm{cos}{q}\int_{−\infty} ^{+\infty} \frac{{x}^{\mathrm{2}} \mathrm{cos}\left({px}\right)}{{x}^{\mathrm{2}} +\left({p}+{q}\right)^{\mathrm{2}} }{dx} \\ $$$$… \\ $$$$\mathrm{now}\:\mathrm{see}\:\mathrm{Q}.\mathrm{132090}\:\mathrm{by}\:\mathrm{rs4090} \\ $$
Answered by mathmax by abdo last updated on 16/Feb/21
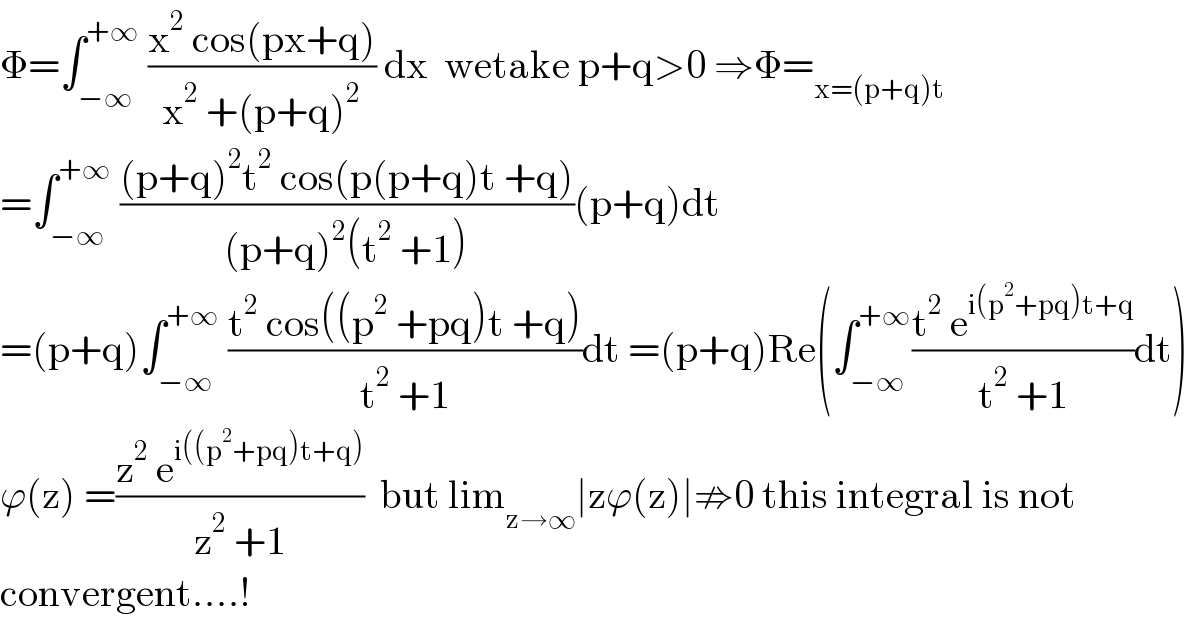
Φ=∫_(−∞) ^(+∞) ((x^2 cos(px+q))/(x^2 +(p+q)^2 )) dx wetake p+q>0 ⇒Φ=_(x=(p+q)t) =∫_(−∞) ^(+∞) (((p+q)^2 t^2 cos(p(p+q)t +q))/((p+q)^2 (t^2 +1)))(p+q)dt =(p+q)∫_(−∞) ^(+∞) ((t^2 cos((p^2 +pq)t +q))/(t^2 +1))dt =(p+q)Re(∫_(−∞) ^(+∞) ((t^2 e^(i(p^2 +pq)t+q) )/(t^2 +1))dt) ϕ(z) =((z^2 e^(i((p^2 +pq)t+q)) )/(z^2 +1)) but lim_(z→∞) ∣zϕ(z)∣⇏0 this integral is not convergent....!
$$\Phi=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{cos}\left(\mathrm{px}+\mathrm{q}\right)}{\mathrm{x}^{\mathrm{2}} \:+\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} }\:\mathrm{dx}\:\:\mathrm{wetake}\:\mathrm{p}+\mathrm{q}>\mathrm{0}\:\Rightarrow\Phi=_{\mathrm{x}=\left(\mathrm{p}+\mathrm{q}\right)\mathrm{t}} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} \:\mathrm{cos}\left(\mathrm{p}\left(\mathrm{p}+\mathrm{q}\right)\mathrm{t}\:+\mathrm{q}\right)}{\left(\mathrm{p}+\mathrm{q}\right)^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\left(\mathrm{p}+\mathrm{q}\right)\mathrm{dt} \\ $$$$=\left(\mathrm{p}+\mathrm{q}\right)\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{2}} \:\mathrm{cos}\left(\left(\mathrm{p}^{\mathrm{2}} \:+\mathrm{pq}\right)\mathrm{t}\:+\mathrm{q}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\left(\mathrm{p}+\mathrm{q}\right)\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \frac{\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{p}^{\mathrm{2}} +\mathrm{pq}\right)\mathrm{t}+\mathrm{q}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right) \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{i}\left(\left(\mathrm{p}^{\mathrm{2}} +\mathrm{pq}\right)\mathrm{t}+\mathrm{q}\right)} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:\mathrm{but}\:\mathrm{lim}_{\mathrm{z}\rightarrow\infty} \mid\mathrm{z}\varphi\left(\mathrm{z}\right)\mid\nRightarrow\mathrm{0}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{convergent}….! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *