Question Number 19192 by Tinkutara last updated on 06/Aug/17
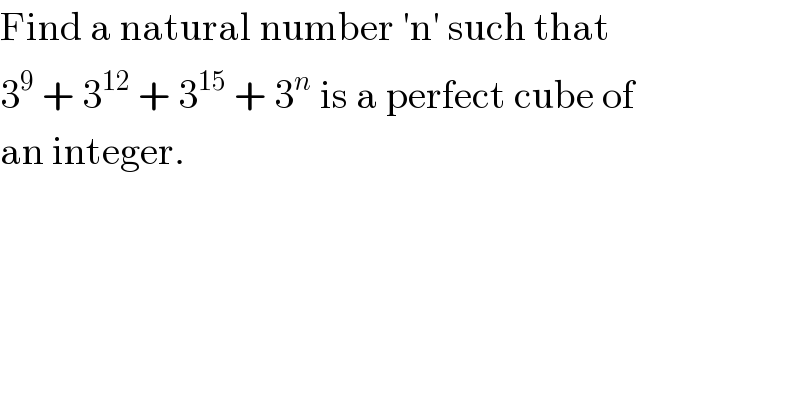
$$\mathrm{Find}\:\mathrm{a}\:\mathrm{natural}\:\mathrm{number}\:'\mathrm{n}'\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{3}^{\mathrm{9}} \:+\:\mathrm{3}^{\mathrm{12}} \:+\:\mathrm{3}^{\mathrm{15}} \:+\:\mathrm{3}^{{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{perfect}\:\mathrm{cube}\:\mathrm{of} \\ $$$$\mathrm{an}\:\mathrm{integer}. \\ $$
Commented by Tinkutara last updated on 07/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by RasheedSindhi last updated on 07/Aug/17
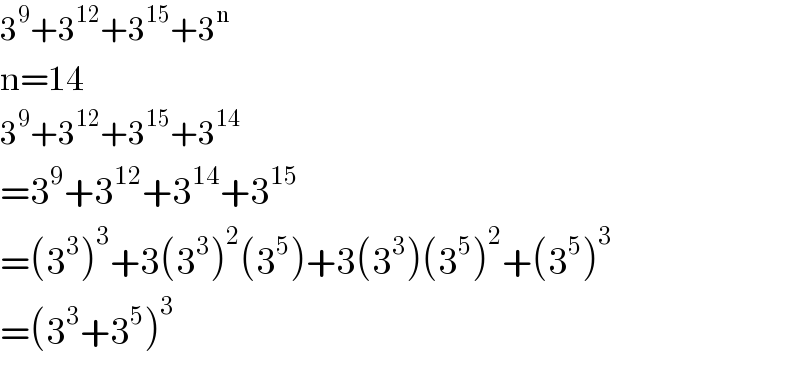
$$\mathrm{3}^{\mathrm{9}} +\mathrm{3}^{\mathrm{12}} +\mathrm{3}^{\mathrm{15}} +\mathrm{3}^{\mathrm{n}} \\ $$$$\mathrm{n}=\mathrm{14} \\ $$$$\mathrm{3}^{\mathrm{9}} +\mathrm{3}^{\mathrm{12}} +\mathrm{3}^{\mathrm{15}} +\mathrm{3}^{\mathrm{14}} \\ $$$$=\mathrm{3}^{\mathrm{9}} +\mathrm{3}^{\mathrm{12}} +\mathrm{3}^{\mathrm{14}} +\mathrm{3}^{\mathrm{15}} \\ $$$$=\left(\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{3}^{\mathrm{3}} \right)^{\mathrm{2}} \left(\mathrm{3}^{\mathrm{5}} \right)+\mathrm{3}\left(\mathrm{3}^{\mathrm{3}} \right)\left(\mathrm{3}^{\mathrm{5}} \right)^{\mathrm{2}} +\left(\mathrm{3}^{\mathrm{5}} \right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{3}^{\mathrm{3}} +\mathrm{3}^{\mathrm{5}} \right)^{\mathrm{3}} \\ $$
