Menu Close

Let-f-x-be-a-quadratic-polynomial-with-integer-coefficients-such-that-f-0-and-f-1-are-odd-integers-Prove-that-the-equation-f-x-0-does-not-have-an-integer-solution-

Tinku Tara 0 Comments
Pin




Question Number 19245 by Tinkutara last updated on 07/Aug/17
Let f(x) be a quadratic polynomial with integer coefficients such that f(0) and f(1) are odd integers. Prove that the equation f(x) = 0 does not have an integer solution.
$$\mathrm{Let}\:{f}\left({x}\right)\:\mathrm{be}\:\mathrm{a}\:\mathrm{quadratic}\:\mathrm{polynomial} \\ $$$$\mathrm{with}\:\mathrm{integer}\:\mathrm{coefficients}\:\mathrm{such}\:\mathrm{that}\:{f}\left(\mathrm{0}\right) \\ $$$$\mathrm{and}\:{f}\left(\mathrm{1}\right)\:\mathrm{are}\:\mathrm{odd}\:\mathrm{integers}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{equation}\:{f}\left({x}\right)\:=\:\mathrm{0}\:\mathrm{does}\:\mathrm{not}\:\mathrm{have}\:\mathrm{an} \\ $$$$\mathrm{integer}\:\mathrm{solution}. \\ $$
Commented by RasheedSindhi last updated on 08/Aug/17
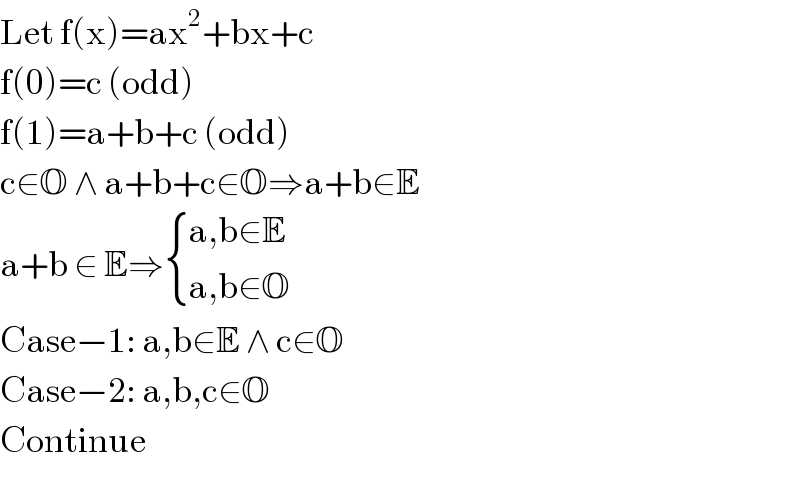
Let f(x)=ax^2 +bx+c f(0)=c (odd) f(1)=a+b+c (odd) c∈O ∧ a+b+c∈O⇒a+b∈E a+b ∈ E⇒ { ((a,b∈E)),((a,b∈O)) :} Case−1: a,b∈E ∧ c∈O Case−2: a,b,c∈O Continue
$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{c}\:\left(\mathrm{odd}\right) \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{a}+\mathrm{b}+\mathrm{c}\:\left(\mathrm{odd}\right) \\ $$$$\mathrm{c}\in\mathbb{O}\:\wedge\:\mathrm{a}+\mathrm{b}+\mathrm{c}\in\mathbb{O}\Rightarrow\mathrm{a}+\mathrm{b}\in\mathbb{E} \\ $$$$\mathrm{a}+\mathrm{b}\:\in\:\mathbb{E}\Rightarrow\begin{cases}{\mathrm{a},\mathrm{b}\in\mathbb{E}}\\{\mathrm{a},\mathrm{b}\in\mathbb{O}}\end{cases} \\ $$$$\mathrm{Case}−\mathrm{1}:\:\mathrm{a},\mathrm{b}\in\mathbb{E}\:\wedge\:\mathrm{c}\in\mathbb{O} \\ $$$$\mathrm{Case}−\mathrm{2}:\:\mathrm{a},\mathrm{b},\mathrm{c}\in\mathbb{O} \\ $$$$\mathrm{Continue} \\ $$
Answered by RasheedSindhi last updated on 09/Aug/17
Quadratic polynomial whose roots are p and q is f(x)=x^2 −(p+q)x+pq f(0)=pq∈O(given)⇒p,q∈O f(1)=1−(p+q)+pq∈O(given) But p,q∈O⇒p+q∈E and f(1)=1−(p+q)+pq∈O ⇒(odd)−(even)+(odd) ⇒(odd)+(odd)=(even)∉O This contradiction proves that p and q are neither odd nor even or they are not integers.
$$\mathrm{Quadratic}\:\mathrm{polynomial}\:\mathrm{whose}\:\mathrm{roots} \\ $$$$\mathrm{are}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{is} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\left(\mathrm{p}+\mathrm{q}\right)\mathrm{x}+\mathrm{pq} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{pq}\in\mathbb{O}\left(\mathrm{given}\right)\Rightarrow\mathrm{p},\mathrm{q}\in\mathbb{O} \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1}−\left(\mathrm{p}+\mathrm{q}\right)+\mathrm{pq}\in\mathbb{O}\left(\mathrm{given}\right) \\ $$$$\mathrm{But} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{p},\mathrm{q}\in\mathbb{O}\Rightarrow\mathrm{p}+\mathrm{q}\in\mathbb{E}\:\:\mathrm{and} \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{1}−\left(\mathrm{p}+\mathrm{q}\right)+\mathrm{pq}\in\mathbb{O} \\ $$$$\:\:\:\:\Rightarrow\left(\mathrm{odd}\right)−\left(\mathrm{even}\right)+\left(\mathrm{odd}\right) \\ $$$$\:\:\:\:\Rightarrow\left(\mathrm{odd}\right)+\left(\mathrm{odd}\right)=\left(\mathrm{even}\right)\notin\mathbb{O} \\ $$$$\mathrm{This}\:\mathrm{contradiction}\:\mathrm{proves} \\ $$$$\mathrm{that}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{are}\:\mathrm{neither}\:\mathrm{odd} \\ $$$$\mathrm{nor}\:\mathrm{even}\:\mathrm{or}\:\mathrm{they}\:\mathrm{are}\:\mathrm{not}\:\mathrm{integers}. \\ $$
Commented by Tinkutara last updated on 09/Aug/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *