Solve-0-pi-2-cos-2-x-ln-cot-x-dx-m-n-

Question Number 150325 by mnjuly1970 last updated on 11/Aug/21

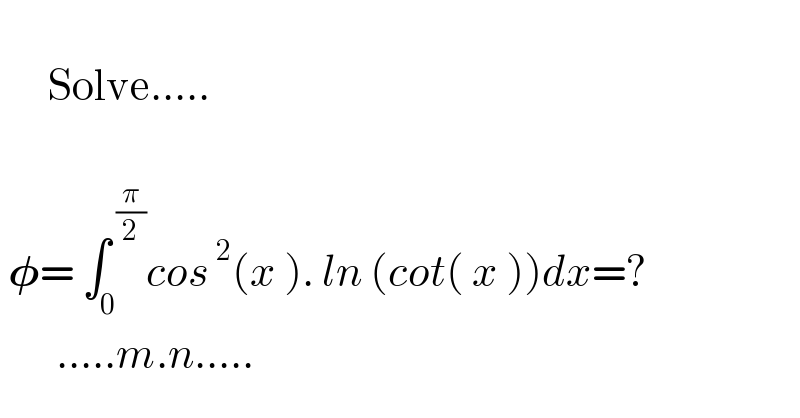
Solve..... 𝛗= ∫_0 ^( (π/2)) cos^( 2) (x ). ln (cot( x ))dx=? .....m.n.....

$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\mathrm{Solve}….. \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\boldsymbol{\phi}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {cos}^{\:\mathrm{2}} \left({x}\:\right).\:{ln}\:\left({cot}\left(\:{x}\:\right)\right){dx}=?\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:…..{m}.{n}….. \\ $$

Answered by Ar Brandon last updated on 11/Aug/21

𝛗=∫_0 ^(π/2) cos^2 x∙ln(cotx)dx =∫_0 ^(π/2) cos^2 x∙ln(cosx)dx−∫_0 ^(π/2) cos^2 x∙ln(sinx)dx =(∂/∂α)∣_(α=2) ∫_0 ^(π/2) cos^α xdx−(∂/∂α)∣_(α=0) ∫_0 ^(π/2) cos^2 x∙sin^α xdx =(∂/∂α)∣_(α=2) β(((α+1)/2), (1/2))−(∂/∂α)∣_(α=0) β((3/2), ((α+1)/2)) =(∂/∂α)∣_(α=2) ((Γ(((α+1)/2))Γ((1/2)))/(Γ((α/2)+1)))−(∂/∂α)∣_(α=0) ((Γ((3/2))Γ(((α+1)/2)))/(Γ((α/2)+2))) =((√π)/2)∙∣_(α=2) ((Γ(((α+1)/2))Γ((α/2)+1)[ψ(((α+1)/2))−ψ((α/2)+1)])/(Γ^2 ((α/2)+1))) −((√π)/4)∣_(α=0) ((Γ(((α+1)/2))Γ((α/2)+2)[ψ(((α+1)/2))−ψ((α/2)+2)])/(Γ^2 ((α/2)+2))) =((√π)/2)∙((Γ((3/2))Γ(2)[ψ((3/2))−ψ(2)])/(Γ^2 (2)))−((√π)/4)∙((Γ((1/2))Γ(2)[ψ((1/2))−ψ(2)])/(Γ^2 (2))) =(π/4)(2−γ−2ln2−1+γ)−(π/4)(−γ−2ln2−1+γ) =(π/4)(1−2ln2+1+2ln2)=(π/2)

$$\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {x}\centerdot\mathrm{ln}\left(\mathrm{cot}{x}\right){dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {x}\centerdot\mathrm{ln}\left(\mathrm{cos}{x}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {x}\centerdot\mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$$\:\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\alpha} {xdx}−\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} {x}\centerdot\mathrm{sin}^{\alpha} {xdx} \\ $$$$\:\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \beta\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \beta\left(\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)}−\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{0}} \frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\right)} \\ $$$$\:\:\:\:\:=\frac{\sqrt{\pi}}{\mathrm{2}}\centerdot\mid_{\alpha=\mathrm{2}} \frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)\left[\psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)\right]}{\Gamma^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\frac{\sqrt{\pi}}{\mathrm{4}}\mid_{\alpha=\mathrm{0}} \frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\right)\left[\psi\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\right)\right]}{\Gamma^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}+\mathrm{2}\right)} \\ $$$$\:\:\:\:\:=\frac{\sqrt{\pi}}{\mathrm{2}}\centerdot\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\mathrm{2}\right)\left[\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{2}\right)\right]}{\Gamma^{\mathrm{2}} \left(\mathrm{2}\right)}−\frac{\sqrt{\pi}}{\mathrm{4}}\centerdot\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{2}\right)\left[\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\mathrm{2}\right)\right]}{\Gamma^{\mathrm{2}} \left(\mathrm{2}\right)} \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{2}−\gamma−\mathrm{2ln2}−\mathrm{1}+\gamma\right)−\frac{\pi}{\mathrm{4}}\left(−\gamma−\mathrm{2ln2}−\mathrm{1}+\gamma\right) \\ $$$$\:\:\:\:\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}−\mathrm{2ln2}+\mathrm{1}+\mathrm{2ln2}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 11/Aug/21

$$\:\:\:{thanks}\:{a}\:{lot}\:{sir}\:{brandon}.. \\ $$

Answered by mnjuly1970 last updated on 11/Aug/21

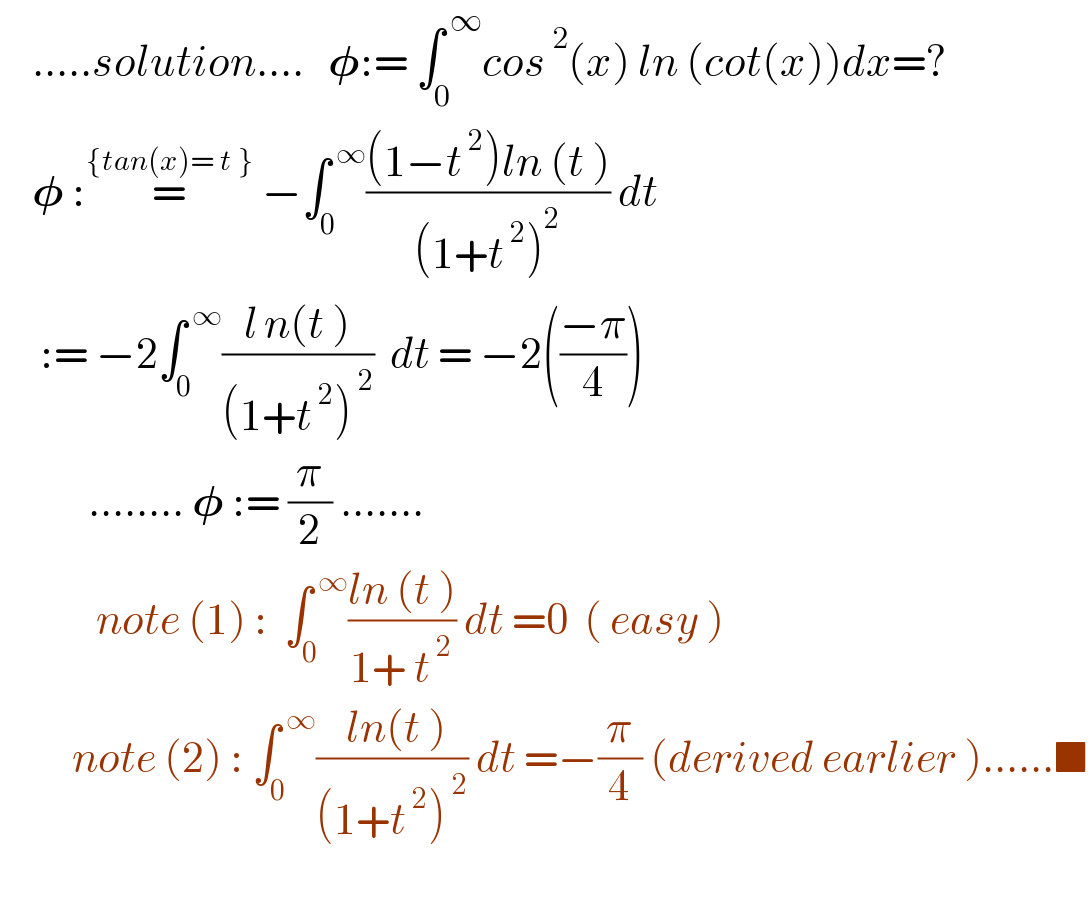
.....solution.... 𝛗:= ∫_0 ^( ∞) cos^( 2) (x) ln (cot(x))dx=? 𝛗 :=^({tan(x)= t }) −∫_0 ^( ∞) (((1−t^( 2) )ln (t ))/((1+t^( 2) )^2 )) dt := −2∫_0 ^( ∞) ((l^ n(t ))/((1+t^( 2) )^( 2) )) dt = −2(((−π)/4)) ........ 𝛗 := (π/2) ....... note (1) : ∫_0 ^( ∞) ((ln (t ))/(1+ t^( 2) )) dt =0 ( easy ) note (2) : ∫_0 ^( ∞) (( ln(t ))/((1+t^( 2) )^( 2) )) dt =−(π/4) (derived earlier )......■

$$\:\:\:\:…..{solution}….\:\:\:\boldsymbol{\phi}:=\:\int_{\mathrm{0}} ^{\:\infty} {cos}^{\:\mathrm{2}} \left({x}\right)\:{ln}\:\left({cot}\left({x}\right)\right){dx}=? \\ $$$$\:\:\:\:\boldsymbol{\phi}\::\overset{\left\{{tan}\left({x}\right)=\:{t}\:\right\}} {=}\:−\int_{\mathrm{0}} ^{\:\infty} \frac{\left(\mathrm{1}−{t}^{\:\mathrm{2}} \right){ln}\:\left({t}\:\right)}{\left(\mathrm{1}+{t}^{\:\mathrm{2}} \right)^{\mathrm{2}} }\:{dt} \\ $$$$\:\:\:\:\::=\:−\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{{l}^{\:} {n}\left({t}\:\right)}{\left(\mathrm{1}+{t}^{\:\mathrm{2}} \right)^{\:\mathrm{2}} }\:\:{dt}\:=\:−\mathrm{2}\left(\frac{−\pi}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:……..\:\boldsymbol{\phi}\::=\:\frac{\pi}{\mathrm{2}}\:……. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{note}\:\left(\mathrm{1}\right)\::\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\:\left({t}\:\right)}{\mathrm{1}+\:{t}^{\:\mathrm{2}} }\:{dt}\:=\mathrm{0}\:\:\left(\:{easy}\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:{note}\:\left(\mathrm{2}\right)\::\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{ln}\left({t}\:\right)}{\left(\mathrm{1}+{t}^{\:\mathrm{2}} \right)^{\:\mathrm{2}} }\:{dt}\:=−\frac{\pi}{\mathrm{4}}\:\left({derived}\:{earlier}\:\right)……\blacksquare \\ $$$$ \\ $$

Facebook Tweet Pin

Solve-0-pi-2-cos-2-x-ln-cot-x-dx-m-n-

Leave a Reply Cancel reply