Menu Close

Question-150410

Tinku Tara 0 Comments
Pin




Question Number 150410 by ajfour last updated on 12/Aug/21
Commented by ajfour last updated on 12/Aug/21
If length of cylinder and both width and length of wedge are equal, and that their material densities are even equal, and their acceleration magnitudes (from ground reference) are equal then find x/r. (assume pure rolling).
$${If}\:{length}\:{of}\:{cylinder}\:{and} \\ $$$${both}\:{width}\:{and}\:{length}\:{of} \\ $$$${wedge}\:{are}\:{equal},\:{and}\:{that} \\ $$$${their}\:{material}\:{densities} \\ $$$${are}\:{even}\:{equal},\:{and}\:{their} \\ $$$${acceleration}\:{magnitudes} \\ $$$$\left({from}\:{ground}\:{reference}\right) \\ $$$${are}\:{equal}\:{then}\:{find}\:{x}/{r}. \\ $$$$\left({assume}\:{pure}\:{rolling}\right). \\ $$
Answered by ajfour last updated on 12/Aug/21
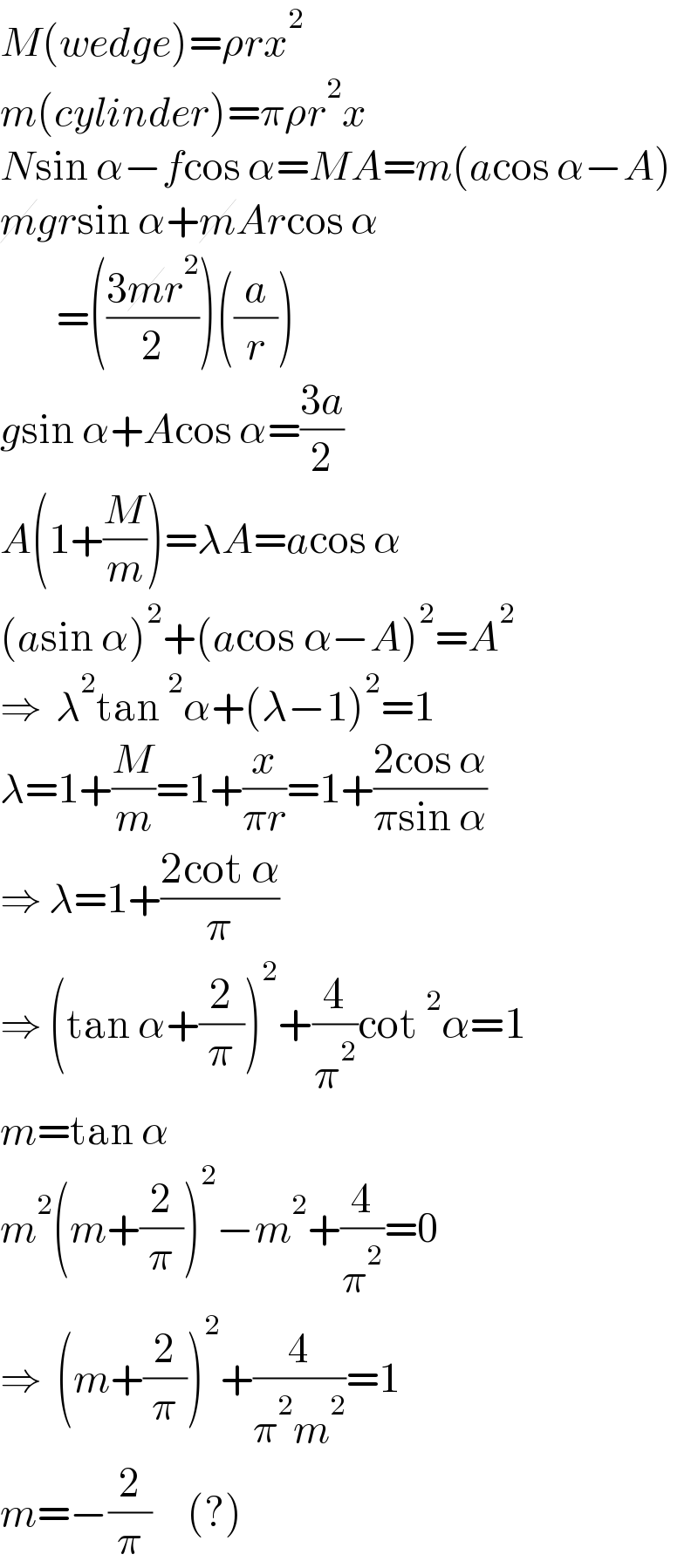
M(wedge)=ρrx^2 m(cylinder)=πρr^2 x Nsin α−fcos α=MA=m(acos α−A) mgrsin α+mArcos α =(((3mr^2 )/2))((a/r)) gsin α+Acos α=((3a)/2) A(1+(M/m))=λA=acos α (asin α)^2 +(acos α−A)^2 =A^2 ⇒ λ^2 tan^2 α+(λ−1)^2 =1 λ=1+(M/m)=1+(x/(πr))=1+((2cos α)/(πsin α)) ⇒ λ=1+((2cot α)/π) ⇒ (tan α+(2/π))^2 +(4/π^2 )cot^2 α=1 m=tan α m^2 (m+(2/π))^2 −m^2 +(4/π^2 )=0 ⇒ (m+(2/π))^2 +(4/(π^2 m^2 ))=1 m=−(2/π) (?)
$${M}\left({wedge}\right)=\rho{rx}^{\mathrm{2}} \\ $$$${m}\left({cylinder}\right)=\pi\rho{r}^{\mathrm{2}} {x} \\ $$$${N}\mathrm{sin}\:\alpha−{f}\mathrm{cos}\:\alpha={MA}={m}\left({a}\mathrm{cos}\:\alpha−{A}\right) \\ $$$$\cancel{{m}gr}\mathrm{sin}\:\alpha+\cancel{{m}Ar}\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{3}\cancel{{m}r}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\frac{{a}}{{r}}\right) \\ $$$${g}\mathrm{sin}\:\alpha+{A}\mathrm{cos}\:\alpha=\frac{\mathrm{3}{a}}{\mathrm{2}} \\ $$$${A}\left(\mathrm{1}+\frac{{M}}{{m}}\right)=\lambda{A}={a}\mathrm{cos}\:\alpha \\ $$$$\left({a}\mathrm{sin}\:\alpha\right)^{\mathrm{2}} +\left({a}\mathrm{cos}\:\alpha−{A}\right)^{\mathrm{2}} ={A}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\lambda^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \alpha+\left(\lambda−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\lambda=\mathrm{1}+\frac{{M}}{{m}}=\mathrm{1}+\frac{{x}}{\pi{r}}=\mathrm{1}+\frac{\mathrm{2cos}\:\alpha}{\pi\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow\:\lambda=\mathrm{1}+\frac{\mathrm{2cot}\:\alpha}{\pi} \\ $$$$\Rightarrow\:\left(\mathrm{tan}\:\alpha+\frac{\mathrm{2}}{\pi}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\pi^{\mathrm{2}} }\mathrm{cot}\:^{\mathrm{2}} \alpha=\mathrm{1} \\ $$$${m}=\mathrm{tan}\:\alpha \\ $$$${m}^{\mathrm{2}} \left({m}+\frac{\mathrm{2}}{\pi}\right)^{\mathrm{2}} −{m}^{\mathrm{2}} +\frac{\mathrm{4}}{\pi^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:\:\left({m}+\frac{\mathrm{2}}{\pi}\right)^{\mathrm{2}} +\frac{\mathrm{4}}{\pi^{\mathrm{2}} {m}^{\mathrm{2}} }=\mathrm{1} \\ $$$${m}=−\frac{\mathrm{2}}{\pi}\:\:\:\:\:\left(?\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *