Question Number 19511 by Tinkutara last updated on 12/Aug/17

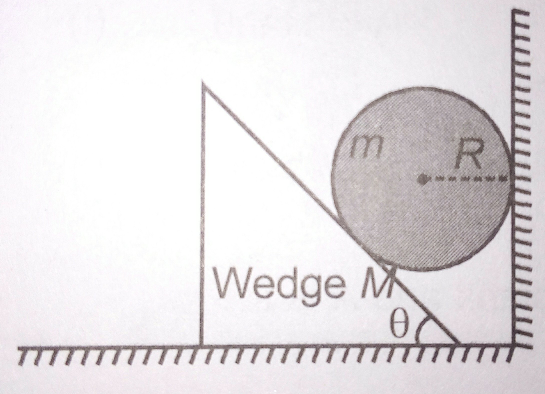
$$\mathrm{In}\:\mathrm{the}\:\mathrm{arrangement}\:\mathrm{shown},\:\mathrm{the}\:\mathrm{wedge} \\ $$$$\mathrm{is}\:\mathrm{smooth}\:\mathrm{and}\:\mathrm{has}\:\mathrm{a}\:\mathrm{mass}\:{M}.\:\mathrm{The}\:\mathrm{sphere} \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{mass}\:{m}.\:\mathrm{The}\:\mathrm{system}\:\mathrm{is}\:\mathrm{released} \\ $$$$\mathrm{from}\:\mathrm{rest}\:\mathrm{from}\:\mathrm{the}\:\mathrm{position}\:\mathrm{shown}. \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{friction}\:\mathrm{anywhere}.\:\mathrm{Find}\:\mathrm{the} \\ $$$$\mathrm{contact}\:\mathrm{force}\:\mathrm{between}\:\mathrm{the}\:\mathrm{wall}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{sphere}. \\ $$
Commented by Tinkutara last updated on 12/Aug/17
Answered by ajfour last updated on 12/Aug/17
Commented by ajfour last updated on 12/Aug/17

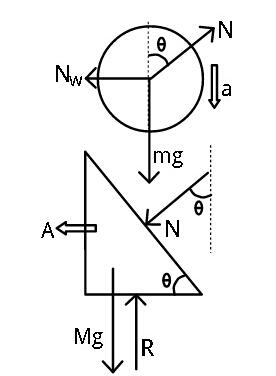
$$\:\:\mathrm{Asin}\:\theta\:=\:\mathrm{acos}\:\theta\:\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$\mathrm{because}\:\mathrm{along}\:\mathrm{the}\:\mathrm{direction}\: \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{incline}\:\mathrm{of}\:\mathrm{wedge} \\ $$$$\mathrm{sphere}\:\mathrm{and}\:\mathrm{wedge}\:\mathrm{maintain}\:\mathrm{contact}. \\ $$$$\:\:\:\mathrm{From}\:\mathrm{diagram}\:\mathrm{of}\:\mathrm{wedge} \\ $$$$\:\:\:\:\:\mathrm{Nsin}\:\theta=\:\mathrm{MA}\:\:\:\:….\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\mathrm{from}\:\mathrm{diagram}\:\mathrm{of}\:\mathrm{sphere} \\ $$$$\:\:\:\:\:\:\:\mathrm{N}_{\mathrm{w}} =\:\mathrm{Nsin}\:\theta\:\:\:\:\:\:\:\:…..\left(\mathrm{iii}\right) \\ $$$$\:\:\mathrm{and}\:\:\:\:\mathrm{mg}−\mathrm{Ncos}\:\theta=\mathrm{ma}\:\:\:….\left(\mathrm{iv}\right) \\ $$$$\mathrm{As}\:\:\:\mathrm{N}_{\mathrm{w}} =\:\mathrm{Nsin}\:\theta=\mathrm{MA} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{from}\:\left(\mathrm{iv}\right) \\ $$$$\:\:\:\:\:\mathrm{mg}−\frac{\mathrm{MAcos}\:\theta}{\mathrm{sin}\:\theta}=\frac{\mathrm{mAsin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\:\:\:\:\mathrm{A}\left(\mathrm{mtan}\:\theta+\mathrm{Mcot}\:\theta\right)=\mathrm{mg} \\ $$$$\mathrm{So},\:\:\boldsymbol{\mathrm{N}}_{\mathrm{w}} =\boldsymbol{\mathrm{MA}}=\frac{\boldsymbol{\mathrm{mMg}}}{\boldsymbol{\mathrm{mtan}}\:\boldsymbol{\theta}+\boldsymbol{\mathrm{Mcot}}\:\boldsymbol{\theta}}\:. \\ $$
Commented by Tinkutara last updated on 12/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
