Menu Close

Question-150804

Tinku Tara 0 Comments
Pin




Question Number 150804 by mathdanisur last updated on 15/Aug/21
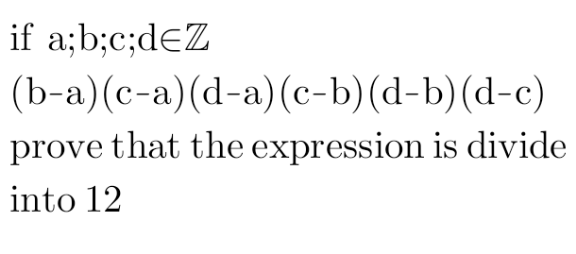
Answered by aleks041103 last updated on 15/Aug/21
Let P=(b−a)(c−a)(d−a)(c−b)(d−b)(d−c). Obviously P is the product of all possible differences between a,b,c,d. 1. Divisibility by 3, i.e. 3∣P. If any two of the four numbers have the same remainder when divided by 3, their difference will have a remainder 0 and therefore it will be divisible by 3. Therefore 3∣P. Since there are exactly 3 possible remainders and we have 4 numbers, it′s unavoidable to have at least two numbers with the same remainder. Therefore 3∣P. 2. Divisibility by 4, i.e. 4∣P. The same argument as in 1. shows that if 2 of the 4 numbers have the same remainder when divided by 4, then 4∣P. Let all of the 4 numbers have different remainders. Then without any restrictions let a=4A b=4B+1 c=4C+2 d=4D+3 Then: P=(4(B−A)+1)(4(C−A)+2)(4(D−A)+3)(4(C−B)+1)(4(D−B)+2)(4(D−C)+1) But 4(C−A)+2=2(2(C−A)+1) and 4(D−B)+2=2(2(D−B)+1). Then P=4(4(B−A)+1)(4(D−A)+3)(4(C−B)+1)(4(D−C)+1)(2(C−A)+1)(2(D−B)+1) Therefore 4∣P. 3. Divisibility by 12. From 1. and 2. we get: 3∣P and 4∣P and LCM(3,4)=12 ⇒12∣P
$${Let}\:{P}=\left({b}−{a}\right)\left({c}−{a}\right)\left({d}−{a}\right)\left({c}−{b}\right)\left({d}−{b}\right)\left({d}−{c}\right). \\ $$$${Obviously}\:{P}\:\:{is}\:{the}\:{product}\:{of}\:{all} \\ $$$${possible}\:{differences}\:{between}\:{a},{b},{c},{d}. \\ $$$$\mathrm{1}.\:{Divisibility}\:{by}\:\mathrm{3},\:{i}.{e}.\:\mathrm{3}\mid{P}. \\ $$$${If}\:{any}\:{two}\:{of}\:{the}\:{four}\:{numbers} \\ $$$${have}\:{the}\:{same}\:{remainder}\:{when}\:{divided} \\ $$$${by}\:\mathrm{3},\:{their}\:{difference}\:{will}\:{have}\:{a} \\ $$$${remainder}\:\mathrm{0}\:{and}\:{therefore}\:{it}\:{will}\:{be}\:{divisible} \\ $$$${by}\:\mathrm{3}.\:{Therefore}\:\mathrm{3}\mid{P}. \\ $$$${Since}\:{there}\:{are}\:{exactly}\:\mathrm{3}\:{possible}\: \\ $$$${remainders}\:{and}\:{we}\:{have}\:\mathrm{4}\:{numbers}, \\ $$$${it}'{s}\:{unavoidable}\:{to}\:{have}\:{at}\:{least}\:{two} \\ $$$${numbers}\:{with}\:{the}\:{same}\:{remainder}. \\ $$$${Therefore}\:\mathrm{3}\mid{P}. \\ $$$$\mathrm{2}.\:{Divisibility}\:{by}\:\mathrm{4},\:{i}.{e}.\:\mathrm{4}\mid{P}. \\ $$$${The}\:{same}\:{argument}\:{as}\:{in}\:\mathrm{1}.\:{shows}\: \\ $$$${that}\:{if}\:\mathrm{2}\:{of}\:{the}\:\mathrm{4}\:{numbers}\:{have}\:{the} \\ $$$${same}\:{remainder}\:{when}\:{divided}\:{by}\:\mathrm{4}, \\ $$$${then}\:\mathrm{4}\mid{P}. \\ $$$${Let}\:{all}\:{of}\:{the}\:\mathrm{4}\:{numbers}\:{have}\:{different} \\ $$$${remainders}.\:{Then}\:{without}\:{any}\:{restrictions} \\ $$$${let} \\ $$$${a}=\mathrm{4}{A} \\ $$$${b}=\mathrm{4}{B}+\mathrm{1} \\ $$$${c}=\mathrm{4}{C}+\mathrm{2} \\ $$$${d}=\mathrm{4}{D}+\mathrm{3} \\ $$$${Then}: \\ $$$${P}=\left(\mathrm{4}\left({B}−{A}\right)+\mathrm{1}\right)\left(\mathrm{4}\left({C}−{A}\right)+\mathrm{2}\right)\left(\mathrm{4}\left({D}−{A}\right)+\mathrm{3}\right)\left(\mathrm{4}\left({C}−{B}\right)+\mathrm{1}\right)\left(\mathrm{4}\left({D}−{B}\right)+\mathrm{2}\right)\left(\mathrm{4}\left({D}−{C}\right)+\mathrm{1}\right) \\ $$$${But}\:\mathrm{4}\left({C}−{A}\right)+\mathrm{2}=\mathrm{2}\left(\mathrm{2}\left({C}−{A}\right)+\mathrm{1}\right)\:{and} \\ $$$$\mathrm{4}\left({D}−{B}\right)+\mathrm{2}=\mathrm{2}\left(\mathrm{2}\left({D}−{B}\right)+\mathrm{1}\right).\:{Then} \\ $$$${P}=\mathrm{4}\left(\mathrm{4}\left({B}−{A}\right)+\mathrm{1}\right)\left(\mathrm{4}\left({D}−{A}\right)+\mathrm{3}\right)\left(\mathrm{4}\left({C}−{B}\right)+\mathrm{1}\right)\left(\mathrm{4}\left({D}−{C}\right)+\mathrm{1}\right)\left(\mathrm{2}\left({C}−{A}\right)+\mathrm{1}\right)\left(\mathrm{2}\left({D}−{B}\right)+\mathrm{1}\right) \\ $$$${Therefore}\:\mathrm{4}\mid{P}. \\ $$$$\mathrm{3}.\:{Divisibility}\:{by}\:\mathrm{12}. \\ $$$${From}\:\mathrm{1}.\:{and}\:\mathrm{2}.\:{we}\:{get}: \\ $$$$\mathrm{3}\mid{P}\:{and}\:\mathrm{4}\mid{P}\:{and}\:{LCM}\left(\mathrm{3},\mathrm{4}\right)=\mathrm{12} \\ $$$$\Rightarrow\mathrm{12}\mid{P} \\ $$
Commented by mathdanisur last updated on 15/Aug/21
nice Ser thank you
$$\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *