Question Number 151073 by mathdanisur last updated on 18/Aug/21
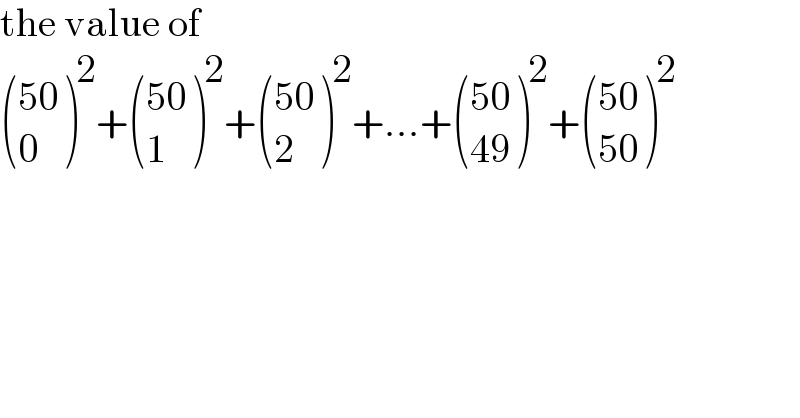
$$\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\begin{pmatrix}{\mathrm{50}}\\{\mathrm{0}}\end{pmatrix}^{\mathrm{2}} +\begin{pmatrix}{\mathrm{50}}\\{\mathrm{1}}\end{pmatrix}^{\mathrm{2}} +\begin{pmatrix}{\mathrm{50}}\\{\mathrm{2}}\end{pmatrix}^{\mathrm{2}} +…+\begin{pmatrix}{\mathrm{50}}\\{\mathrm{49}}\end{pmatrix}^{\mathrm{2}} +\begin{pmatrix}{\mathrm{50}}\\{\mathrm{50}}\end{pmatrix}^{\mathrm{2}} \\ $$
Answered by ArielVyny last updated on 18/Aug/21
![S_n =Σ_(k=0) ^(50) (C_(50) ^k )^2 ln(S_n )=2Σ_(k=0) ^(50) ln(((50!)/(k!(50−k)!)))=2ln(50!)(50+1)−2Σ_(k=0) ^(50) ln[k!(50−k)!] ln(S_n )=102ln(50!)−2Σ_(k=0) ^(50) ln(k!)−2Σ_(k=0) ^(50) ln(50−k)! ln(S_n )=102ln(50!)→S_n =e^(102ln(50!)) =e^(ln(50!)^(102) ) S_n =(50!)^(102)](https://www.tinkutara.com/question/Q151106.png)
$${S}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}\left({C}_{\mathrm{50}} ^{{k}} \right)^{\mathrm{2}} \\ $$$${ln}\left({S}_{{n}} \right)=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}{ln}\left(\frac{\mathrm{50}!}{{k}!\left(\mathrm{50}−{k}\right)!}\right)=\mathrm{2}{ln}\left(\mathrm{50}!\right)\left(\mathrm{50}+\mathrm{1}\right)−\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}{ln}\left[{k}!\left(\mathrm{50}−{k}\right)!\right] \\ $$$${ln}\left({S}_{{n}} \right)=\mathrm{102}{ln}\left(\mathrm{50}!\right)−\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}{ln}\left({k}!\right)−\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\mathrm{50}} {\sum}}{ln}\left(\mathrm{50}−{k}\right)! \\ $$$$ \\ $$$${ln}\left({S}_{{n}} \right)=\mathrm{102}{ln}\left(\mathrm{50}!\right)\rightarrow{S}_{{n}} ={e}^{\mathrm{102}{ln}\left(\mathrm{50}!\right)} ={e}^{{ln}\left(\mathrm{50}!\right)^{\mathrm{102}} } \\ $$$${S}_{{n}} =\left(\mathrm{50}!\right)^{\mathrm{102}} \\ $$
Commented by mathdanisur last updated on 18/Aug/21
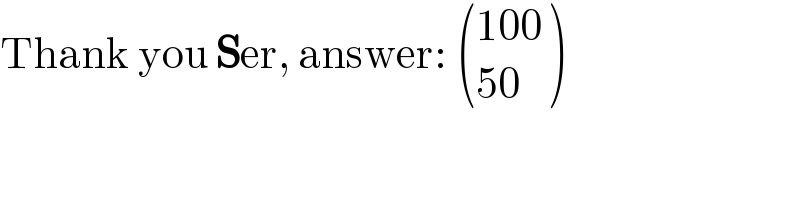
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{answer}:\:\begin{pmatrix}{\mathrm{100}}\\{\mathrm{50}}\end{pmatrix} \\ $$
Commented by mr W last updated on 18/Aug/21
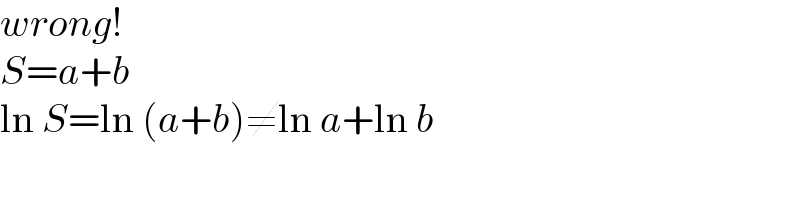
$${wrong}! \\ $$$${S}={a}+{b} \\ $$$$\mathrm{ln}\:{S}=\mathrm{ln}\:\left({a}+{b}\right)\neq\mathrm{ln}\:{a}+\mathrm{ln}\:{b} \\ $$
Answered by mr W last updated on 18/Aug/21
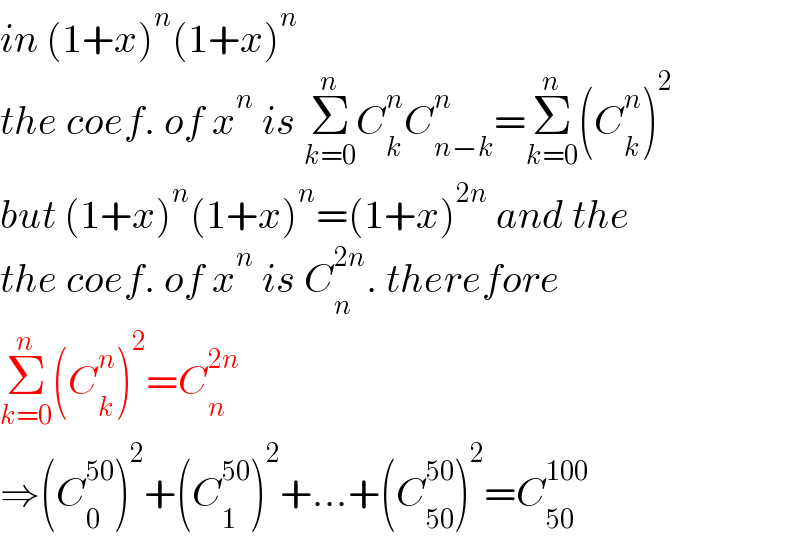
$${in}\:\left(\mathrm{1}+{x}\right)^{{n}} \left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${the}\:{coef}.\:{of}\:{x}^{{n}} \:{is}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} {C}_{{n}−{k}} ^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({C}_{{k}} ^{{n}} \right)^{\mathrm{2}} \\ $$$${but}\:\left(\mathrm{1}+{x}\right)^{{n}} \left(\mathrm{1}+{x}\right)^{{n}} =\left(\mathrm{1}+{x}\right)^{\mathrm{2}{n}} \:{and}\:{the} \\ $$$${the}\:{coef}.\:{of}\:{x}^{{n}} \:{is}\:{C}_{{n}} ^{\mathrm{2}{n}} .\:{therefore} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({C}_{{k}} ^{{n}} \right)^{\mathrm{2}} ={C}_{{n}} ^{\mathrm{2}{n}} \\ $$$$\Rightarrow\left({C}_{\mathrm{0}} ^{\mathrm{50}} \right)^{\mathrm{2}} +\left({C}_{\mathrm{1}} ^{\mathrm{50}} \right)^{\mathrm{2}} +…+\left({C}_{\mathrm{50}} ^{\mathrm{50}} \right)^{\mathrm{2}} ={C}_{\mathrm{50}} ^{\mathrm{100}} \\ $$
Commented by mathdanisur last updated on 18/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
