Question Number 20102 by ajfour last updated on 21/Aug/17
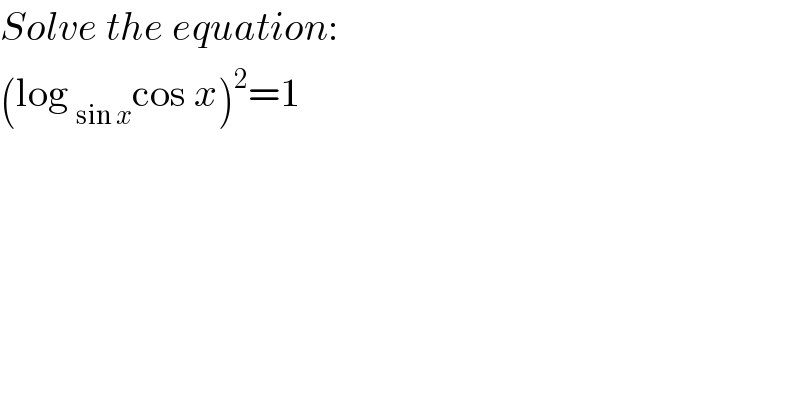
$${Solve}\:{the}\:{equation}: \\ $$$$\left(\mathrm{log}\:_{\mathrm{sin}\:{x}} \mathrm{cos}\:{x}\right)^{\mathrm{2}} =\mathrm{1} \\ $$
Answered by allizzwell23 last updated on 21/Aug/17

$$\:\:\mathrm{log}_{\mathrm{sin}\:{x}} \mathrm{cos}\:{x}\:=\:\mathrm{1} \\ $$$$\:\:\mathrm{cos}\:{x}\:=\:\left(\mathrm{sin}\:{x}\right) \\ $$$$\:\:\mathrm{cos}\:{x}\:=\:\mathrm{sin}\:{x} \\ $$$$\:\:{x}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 21/Aug/17
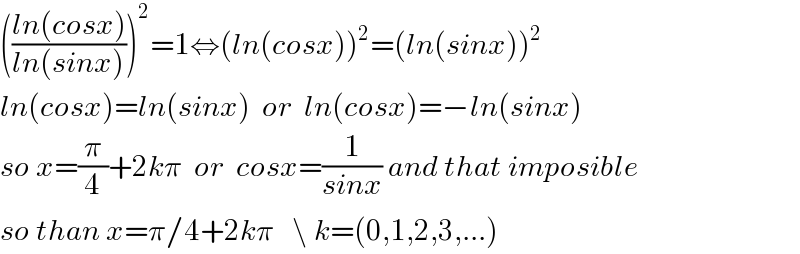
$$\left(\frac{{ln}\left({cosx}\right)}{{ln}\left({sinx}\right)}\right)^{\mathrm{2}} =\mathrm{1}\Leftrightarrow\left({ln}\left({cosx}\right)\right)^{\mathrm{2}} =\left({ln}\left({sinx}\right)\right)^{\mathrm{2}} \\ $$$${ln}\left({cosx}\right)={ln}\left({sinx}\right)\:\:{or}\:\:{ln}\left({cosx}\right)=−{ln}\left({sinx}\right) \\ $$$${so}\:{x}=\frac{\pi}{\mathrm{4}}+\mathrm{2}{k}\pi\:\:{or}\:\:{cosx}=\frac{\mathrm{1}}{{sinx}}\:{and}\:{that}\:{imposible} \\ $$$${so}\:{than}\:{x}=\pi/\mathrm{4}+\mathrm{2}{k}\pi\:\:\:\backslash\:{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},…\right) \\ $$
Commented by sma3l2996 last updated on 21/Aug/17

$${you}\:{welcome} \\ $$
Commented by ajfour last updated on 21/Aug/17

$${thanks}\:{sir},\:{for}\:{general}\:{solution}. \\ $$
