Question Number 151428 by peter frank last updated on 21/Aug/21
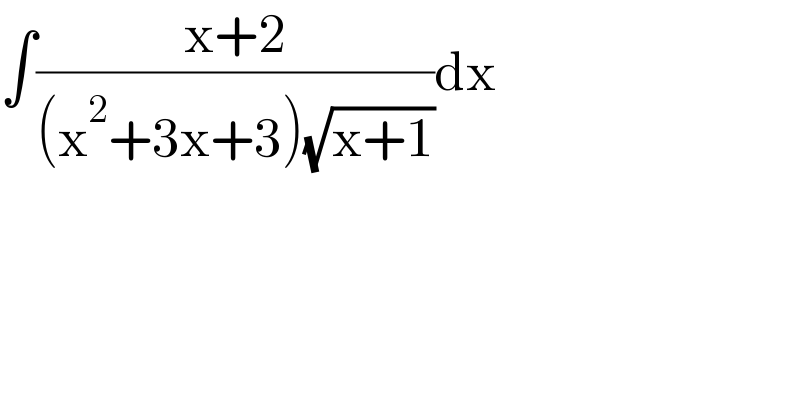
$$\int\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{3}\right)\sqrt{\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$ \\ $$
Answered by MJS_new last updated on 21/Aug/21
![(1) trying something (d/dx)[aarctan (((√(x+1))/(f(x))))]=a((f(x)−2(x+1)f ′(x))/(2(x+1+f(x)^2 )(√(x+1)))) ⇒ a((f(x)−2(x+1)f ′(x))/(2(x+1+f(x)^2 )))=((x+2)/(x^2 +3x+3)) let f(x)=bx+c ⇒ by transforming and comparing constants I get a=±((2(√3))/3)∧b=∓((√3)/3)∧c=0 ⇒ ∫((x+2)/((x^2 +3x+3)(√(x+1))))dx=−((2(√3))/3)arctan ((√(3(x+1)))/x) +C (2) usual Method ∫((x+2)/((x^2 +3x+3)(√(x+1))))dx= [t=(√(x+1)) → dx=2(√(x+1))dt] =2∫((t^2 +1)/(t^4 +t^2 +1))dt=∫(dt/(t^2 −t+1))+∫(dt/(t^2 +t+1))= ... =((2(√3))/3)(arctan ((2t−1)/( (√3))) +arctan ((2t+1)/( (√3))))= =((2(√3))/3)(arctan ((1+2(√(x+1)))/( (√3))) −arctan ((1−2(√(x+1)))/( (√3))))+C](https://www.tinkutara.com/question/Q151438.png)
$$\left(\mathrm{1}\right)\:\mathrm{trying}\:\mathrm{something} \\ $$$$\frac{{d}}{{dx}}\left[{a}\mathrm{arctan}\:\left(\frac{\sqrt{{x}+\mathrm{1}}}{{f}\left({x}\right)}\right)\right]={a}\frac{{f}\left({x}\right)−\mathrm{2}\left({x}+\mathrm{1}\right){f}\:'\left({x}\right)}{\mathrm{2}\left({x}+\mathrm{1}+{f}\left({x}\right)^{\mathrm{2}} \right)\sqrt{{x}+\mathrm{1}}} \\ $$$$\Rightarrow\:{a}\frac{{f}\left({x}\right)−\mathrm{2}\left({x}+\mathrm{1}\right){f}\:'\left({x}\right)}{\mathrm{2}\left({x}+\mathrm{1}+{f}\left({x}\right)^{\mathrm{2}} \right)}=\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}} \\ $$$$\mathrm{let}\:{f}\left({x}\right)={bx}+{c}\:\Rightarrow\:\mathrm{by}\:\mathrm{transforming}\:\mathrm{and} \\ $$$$\mathrm{comparing}\:\mathrm{constants}\:\mathrm{I}\:\mathrm{get} \\ $$$${a}=\pm\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\wedge{b}=\mp\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\wedge{c}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}+\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\right)\sqrt{{x}+\mathrm{1}}}{dx}=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}\left({x}+\mathrm{1}\right)}}{{x}}\:+{C} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{usual}\:\mathrm{Method} \\ $$$$\int\frac{{x}+\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\right)\sqrt{{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}+\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}+\mathrm{1}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\int\frac{{dt}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}+\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}= \\ $$$$… \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{arctan}\:\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:+\mathrm{arctan}\:\frac{\mathrm{2}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)= \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{arctan}\:\frac{\mathrm{1}+\mathrm{2}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\:−\mathrm{arctan}\:\frac{\mathrm{1}−\mathrm{2}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$
