Question Number 67345 by Aditya789 last updated on 26/Aug/19
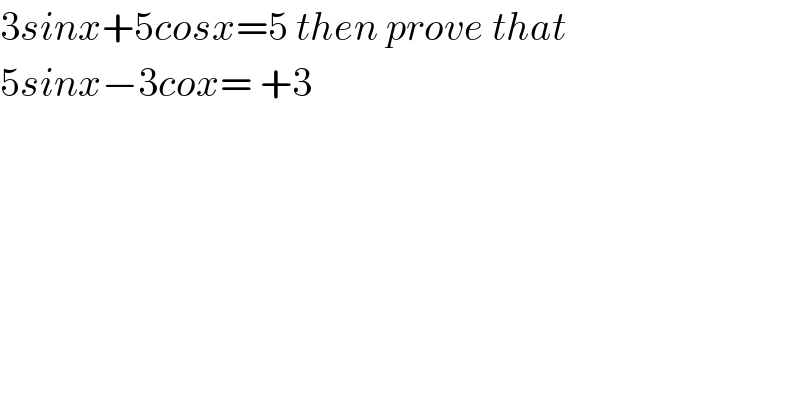
$$\mathrm{3}{sinx}+\mathrm{5}{cosx}=\mathrm{5}\:{then}\:{prove}\:{that}\: \\ $$$$\mathrm{5}{sinx}−\mathrm{3}{cox}=\:+\mathrm{3} \\ $$
Answered by $@ty@m123 last updated on 26/Aug/19
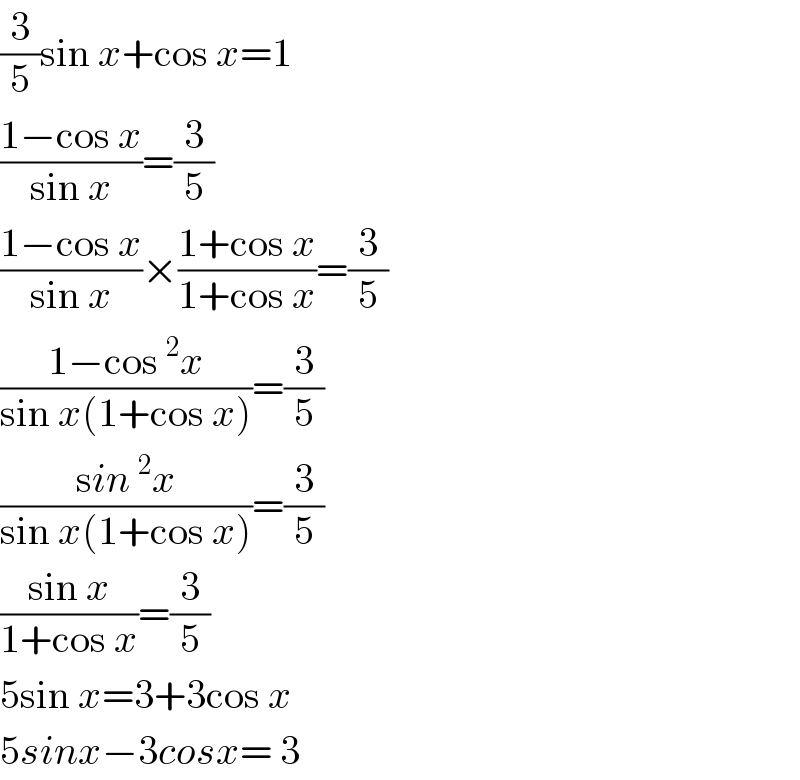
$$\frac{\mathrm{3}}{\mathrm{5}}\mathrm{sin}\:{x}+\mathrm{cos}\:{x}=\mathrm{1} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}×\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\mathrm{s}{in}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\frac{\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{5sin}\:{x}=\mathrm{3}+\mathrm{3cos}\:{x} \\ $$$$\mathrm{5}{sinx}−\mathrm{3}{cosx}=\:\mathrm{3} \\ $$
