Integers-1-2-3-n-where-n-gt-2-are-written-on-a-board-Two-numbers-m-k-such-that-1-lt-m-lt-n-1-lt-k-lt-n-are-removed-and-the-average-of-the-remaining-numbers-is-found-to-be-17-W

Question Number 20693 by Tinkutara last updated on 31/Aug/17

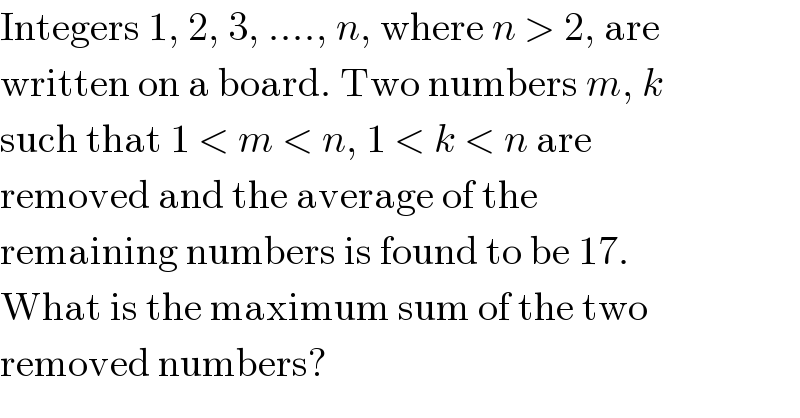
Integers 1, 2, 3, ...., n, where n > 2, are written on a board. Two numbers m, k such that 1 < m < n, 1 < k < n are removed and the average of the remaining numbers is found to be 17. What is the maximum sum of the two removed numbers?

$$\mathrm{Integers}\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:….,\:{n},\:\mathrm{where}\:{n}\:>\:\mathrm{2},\:\mathrm{are} \\ $$$$\mathrm{written}\:\mathrm{on}\:\mathrm{a}\:\mathrm{board}.\:\mathrm{Two}\:\mathrm{numbers}\:{m},\:{k} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{1}\:<\:{m}\:<\:{n},\:\mathrm{1}\:<\:{k}\:<\:{n}\:\mathrm{are} \\ $$$$\mathrm{removed}\:\mathrm{and}\:\mathrm{the}\:\mathrm{average}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{remaining}\:\mathrm{numbers}\:\mathrm{is}\:\mathrm{found}\:\mathrm{to}\:\mathrm{be}\:\mathrm{17}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two} \\ $$$$\mathrm{removed}\:\mathrm{numbers}? \\ $$

Answered by ajfour last updated on 31/Aug/17

(m+k)_(maximum) = 51 ((n(n+1))/2)−(m+k)=17(n−2) ⇒ m+k=((n(n+1))/2)−17(n−2)≤ 2n−2 first let us see (n^2 /2)+(n/2)−17n+34−2n+2 ≤ 0 ⇒ n^2 −37n+72 ≤ 0 (n−((37)/2))^2 ≤ (((37)/2))^2 −72 ∣n−((37)/2)∣ ≤ ((1369−288)/4) ∣n−((37)/2)∣ ≤ (√(270.25)) (≈16.48) ⇒ n−18.5 ≤ 16.48 or n=34 m+k = ((n(n+1))/2)−17(n−2) =17×35−17×32 =51 .

$$\left({m}+{k}\right)_{{maximum}} =\:\mathrm{51} \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−\left({m}+{k}\right)=\mathrm{17}\left({n}−\mathrm{2}\right) \\ $$$$\Rightarrow\:\:\:{m}+{k}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−\mathrm{17}\left({n}−\mathrm{2}\right)\leqslant\:\mathrm{2}{n}−\mathrm{2} \\ $$$$\:\:\:\:\:\:{first}\:{let}\:{us}\:{see} \\ $$$$\:\:\:\:\frac{{n}^{\mathrm{2}} }{\mathrm{2}}+\frac{{n}}{\mathrm{2}}−\mathrm{17}{n}+\mathrm{34}−\mathrm{2}{n}+\mathrm{2}\:\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\:\:{n}^{\mathrm{2}} −\mathrm{37}{n}+\mathrm{72}\:\leqslant\:\mathrm{0} \\ $$$$\:\:\:\:\left({n}−\frac{\mathrm{37}}{\mathrm{2}}\right)^{\mathrm{2}} \:\leqslant\:\left(\frac{\mathrm{37}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{72} \\ $$$$\:\:\:\mid{n}−\frac{\mathrm{37}}{\mathrm{2}}\mid\:\leqslant\:\frac{\mathrm{1369}−\mathrm{288}}{\mathrm{4}} \\ $$$$\:\mid{n}−\frac{\mathrm{37}}{\mathrm{2}}\mid\:\leqslant\:\sqrt{\mathrm{270}.\mathrm{25}}\:\:\:\:\:\left(\approx\mathrm{16}.\mathrm{48}\right) \\ $$$$\Rightarrow\:\:\:\:{n}−\mathrm{18}.\mathrm{5}\:\leqslant\:\mathrm{16}.\mathrm{48} \\ $$$${or}\:\:\:{n}=\mathrm{34} \\ $$$$\:\:\:\:\boldsymbol{{m}}+\boldsymbol{{k}}\:=\:\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}+\mathrm{1}\right)}{\mathrm{2}}−\mathrm{17}\left(\boldsymbol{{n}}−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{17}×\mathrm{35}−\mathrm{17}×\mathrm{32} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{51}\:. \\ $$

Commented by Tinkutara last updated on 01/Sep/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Facebook Tweet Pin

Integers-1-2-3-n-where-n-gt-2-are-written-on-a-board-Two-numbers-m-k-such-that-1-lt-m-lt-n-1-lt-k-lt-n-are-removed-and-the-average-of-the-remaining-numbers-is-found-to-be-17-W

Leave a Reply Cancel reply