Question Number 151863 by pticantor last updated on 23/Aug/21
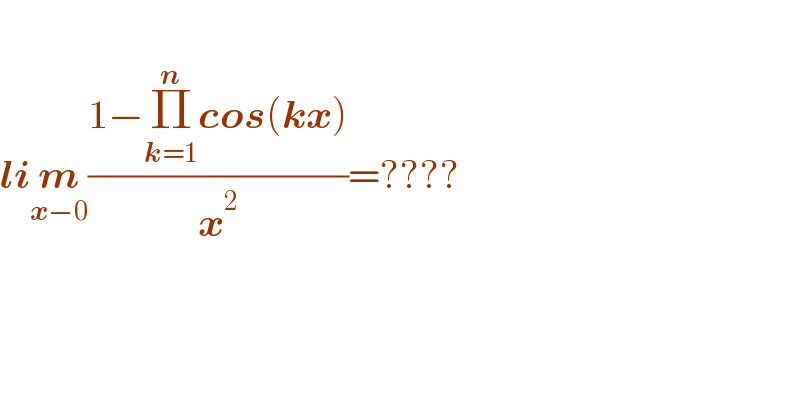
$$\: \\ $$$$\boldsymbol{{li}}\underset{\boldsymbol{{x}}−\mathrm{0}} {\boldsymbol{{m}}}\frac{\mathrm{1}−\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\prod}}\boldsymbol{{cos}}\left(\boldsymbol{{kx}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} }=???? \\ $$$$ \\ $$
Answered by ArielVyny last updated on 23/Aug/21
![Π_(k=1) ^n cos(kx)=Re(Π_(k=1) ^n e^(ikx) ) U_k =Π_(k=1) ^n e^(ikx) →ln(U_k )=Σ_(k=1) ^n ln(e^(ikx) )=Σ_(k≥1) ikx ln(U_k )=ix((n(n+1))/2)→U_k =e^(ix((n(n+1))/2)) Π_(k=1) ^n cos(kx)=cos(((n(n+1))/2)x) lim_(x→0) ((1−cos(((n(n+1))/2)x))/x^2 )=((1−[1−((((((n(n+1))/2)x)^2 )/2)])/x^2 )=((n^2 (n+1)^2 x^2 )/8)×(1/x^2 ) cos(tx)=Σ(((−1)^n (tx)^(2n) )/((2n!)))=1−(((tx)^2 )/2) lim_(x→0) ((1−Π_(k=1) ^n cos(kx))/x^2 )=((n^2 (n+1)^2 )/8)](https://www.tinkutara.com/question/Q151864.png)
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left({kx}\right)={Re}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{e}^{{ikx}} \right) \\ $$$${U}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{e}^{{ikx}} \rightarrow{ln}\left({U}_{{k}} \right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{ln}\left({e}^{{ikx}} \right)=\underset{{k}\geqslant\mathrm{1}} {\sum}{ikx} \\ $$$${ln}\left({U}_{{k}} \right)={ix}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\rightarrow{U}_{{k}} ={e}^{{ix}\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left({kx}\right)={cos}\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}\right) \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cos}\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}\right)}{{x}^{\mathrm{2}} }=\frac{\mathrm{1}−\left[\mathrm{1}−\left(\frac{\left(\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\right]\right.}{{x}^{\mathrm{2}} }=\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{8}}×\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\: \\ $$$${cos}\left({tx}\right)=\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} \left({tx}\right)^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}!\right)}=\mathrm{1}−\frac{\left({tx}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{cos}\left({kx}\right)}{{x}^{\mathrm{2}} }=\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by pticantor last updated on 14/May/22

$$\boldsymbol{{bravooo}} \\ $$
Answered by mnjuly1970 last updated on 24/Aug/21
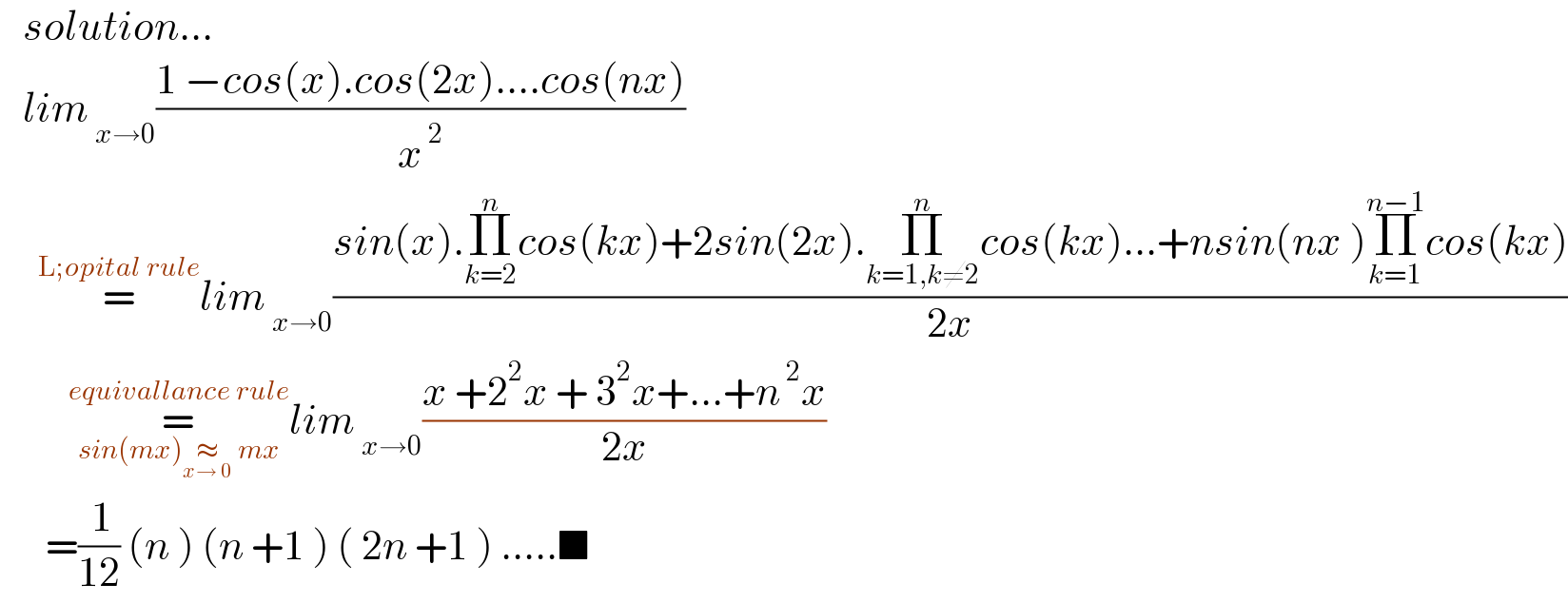
$$\:\:\:{solution}… \\ $$$$\:\:\:{lim}_{\:{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}\:−{cos}\left({x}\right).{cos}\left(\mathrm{2}{x}\right)….{cos}\left({nx}\right)}{{x}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\overset{\mathrm{L};{opital}\:{rule}} {=}{lim}_{\:{x}\rightarrow\mathrm{0}} \frac{{sin}\left({x}\right).\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}{cos}\left({kx}\right)+\mathrm{2}{sin}\left(\mathrm{2}{x}\right).\underset{{k}=\mathrm{1},{k}\neq\mathrm{2}} {\overset{{n}} {\prod}}{cos}\left({kx}\right)…+{nsin}\left({nx}\:\right)\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}{cos}\left({kx}\right)}{\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{sin}\left({mx}\right)\underset{{x}\rightarrow\:\mathrm{0}} {\approx}\:{mx}} {\overset{{equivallance}\:{rule}} {=}}{lim}_{\:{x}\rightarrow\mathrm{0}} \frac{{x}\:+\mathrm{2}^{\mathrm{2}} {x}\:+\:\mathrm{3}^{\mathrm{2}} {x}+…+{n}^{\:\mathrm{2}} {x}}{\mathrm{2}{x}} \\ $$$$\:\:\:\:\:\:=\frac{\:\mathrm{1}}{\mathrm{12}}\:\left({n}\:\right)\:\left({n}\:+\mathrm{1}\:\right)\:\left(\:\mathrm{2}{n}\:+\mathrm{1}\:\right)\:…..\blacksquare \\ $$
