Menu Close

Find-b-b-a-a-dxdy-x-2-y-2-h-2-3-2-

Tinku Tara
Pin




Question Number 131245 by Ahmed1hamouda last updated on 02/Feb/21
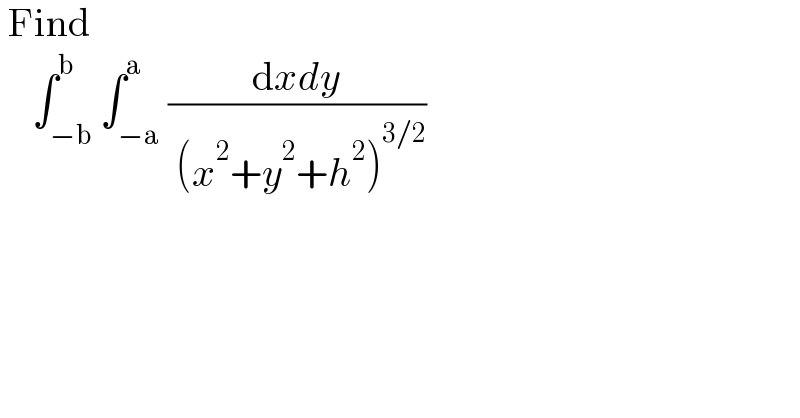
Find ∫_(−b) ^b ∫_(−a) ^a ((dxdy)/( (x^2 +y^2 +h^2 )^(3/2) ))
$$\:\mathrm{Find}\: \\ $$$$\:\:\:\:\int_{−\mathrm{b}} ^{\mathrm{b}} \int_{−\mathrm{a}} ^{\mathrm{a}} \frac{\mathrm{d}{xdy}}{\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{h}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 03/Feb/21
I=∫_(−b) ^b ∫_(−a) ^a ((dxdy)/((x^2 +y^2 +h^2 )^(3/2) ))=4∫_0 ^b ∫_0 ^a ((dxdy)/((x^2 +y^2 +h^2 )^(3/2) )) { ((x=rcosθ),(r∈[0, ∞))),((y=rsinθ),(θ∈[0, 2π])) :} , r=(√(a^2 +b^2 )) ,θ=tan^(−1) ((b/a)) I=4∫_0 ^(tan^(−1) ((b/a))) ∫_0 ^(√(a^2 +b^2 )) ((rdrdθ)/((r^2 +h^2 )^(3/2) )) =−4[(1/((r^2 +h^2 )^(1/2) ))]_0 ^(√(a^2 +b^2 )) ×[(θ/1)]_0 ^(tan^(−1) ((b/a))) =4((1/(∣h∣))−(1/((a^2 +b^2 +h^2 )^(1/2) )))×tan^(−1) ((b/a))
$$\mathcal{I}=\int_{−\mathrm{b}} ^{\mathrm{b}} \int_{−\mathrm{a}} ^{\mathrm{a}} \frac{\mathrm{dxdy}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{b}} \int_{\mathrm{0}} ^{\mathrm{a}} \frac{\mathrm{dxdy}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}&{\mathrm{r}\in\left[\mathrm{0},\:\infty\right)}\\{\mathrm{y}=\mathrm{rsin}\theta}&{\theta\in\left[\mathrm{0},\:\mathrm{2}\pi\right]}\end{cases}\:,\:\mathrm{r}=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\:,\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{a}}\right) \\ $$$$\mathcal{I}=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{a}}\right)} \int_{\mathrm{0}} ^{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} \frac{\mathrm{rdrd}\theta}{\left(\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$\:\:\:=−\mathrm{4}\left[\frac{\mathrm{1}}{\left(\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} }\right]_{\mathrm{0}} ^{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} ×\left[\frac{\theta}{\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{a}}\right)} \\ $$$$\:\:\:=\mathrm{4}\left(\frac{\mathrm{1}}{\mid\mathrm{h}\mid}−\frac{\mathrm{1}}{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} }\right)×\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{b}}{\mathrm{a}}\right) \\ $$
Answered by mathmax by abdo last updated on 03/Feb/21
I =∫_(−b) ^b ∫_(−a) ^a ((dxdy)/((x^2 +y^2 +h^2 )^(3/2) )) ⇒I =4∫_0 ^b .∫_0 ^a ((dxdy)/((x^2 +y^2 +h^2 )^(3/2) )) we consider the diffeomorphism { ((x=rcosθ)),((y=rsinθ)) :} 0≤θ≤2π we have x^2 +y^2 ≤a^2 +b^2 ⇒0≤r≤(√(a^2 +b^2 )) ⇒ I =4 ∫_0 ^(√(a^2 +b^2 )) ∫_0 ^(2π) ((rdrdθ)/((r^2 +h^2 )^(3/2) )) =8π ∫_0 ^(√(a^2 +b^2 )) r(r^2 +h^2 )^(−(3/2)) dr =−8π[(r^2 +h^2 )^(−(1/2)) ]_0 ^(√(a^2 +b^2 )) =−8π{(a^2 +b^2 +h^2 )^(−(1/2)) −h^(−1) } I=8π{(1/h)−(1/( (√(a^2 +b^2 +h^2 ))))}
$$\mathrm{I}\:=\int_{−\mathrm{b}} ^{\mathrm{b}} \:\int_{−\mathrm{a}} ^{\mathrm{a}} \:\frac{\mathrm{dxdy}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \:+\mathrm{h}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\Rightarrow\mathrm{I}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{b}} .\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{dxdy}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \:+\mathrm{h}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\mathrm{we}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{diffeomorphism}\:\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases} \\ $$$$\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi\:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \:\leqslant\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}\leqslant\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{4}\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} \int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{rdrd}\theta}{\left(\mathrm{r}^{\mathrm{2}} \:+\mathrm{h}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\mathrm{8}\pi\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }} \:\:\:\mathrm{r}\left(\mathrm{r}^{\mathrm{2}} \:+\mathrm{h}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{dr} \\ $$$$=−\mathrm{8}\pi\left[\left(\mathrm{r}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\sqrt{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }} \:\:\:=−\mathrm{8}\pi\left\{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} \:+\mathrm{h}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{h}^{−\mathrm{1}} \right\} \\ $$$$\mathrm{I}=\mathrm{8}\pi\left\{\frac{\mathrm{1}}{\mathrm{h}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{h}^{\mathrm{2}} }}\right\} \\ $$

Pin