Question Number 152275 by peter frank last updated on 27/Aug/21
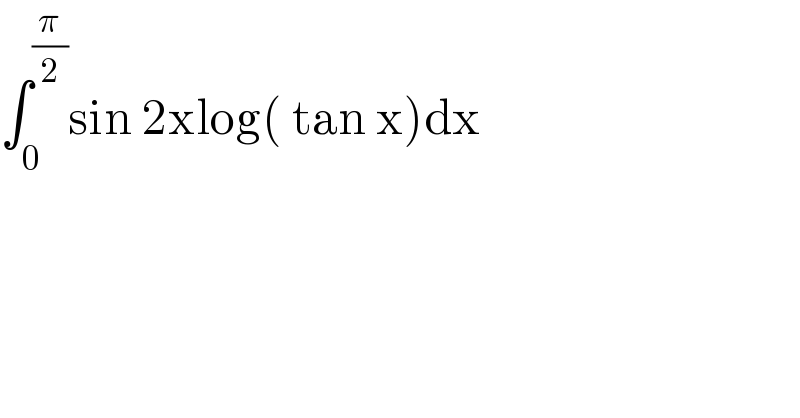
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}\:\mathrm{2xlog}\left(\:\mathrm{tan}\:\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by qaz last updated on 27/Aug/21
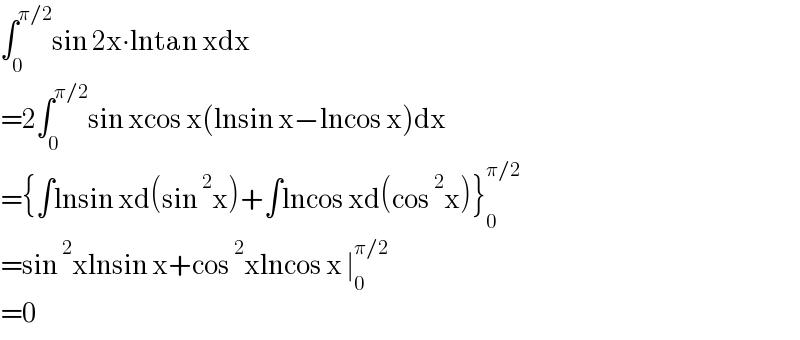
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:\mathrm{2x}\centerdot\mathrm{lntan}\:\mathrm{xdx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}\left(\mathrm{lnsin}\:\mathrm{x}−\mathrm{lncos}\:\mathrm{x}\right)\mathrm{dx} \\ $$$$=\left\{\int\mathrm{lnsin}\:\mathrm{xd}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)+\int\mathrm{lncos}\:\mathrm{xd}\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)\right\}_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\mathrm{sin}\:^{\mathrm{2}} \mathrm{xlnsin}\:\mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{xlncos}\:\mathrm{x}\:\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\mathrm{0} \\ $$
Answered by mnjuly1970 last updated on 27/Aug/21
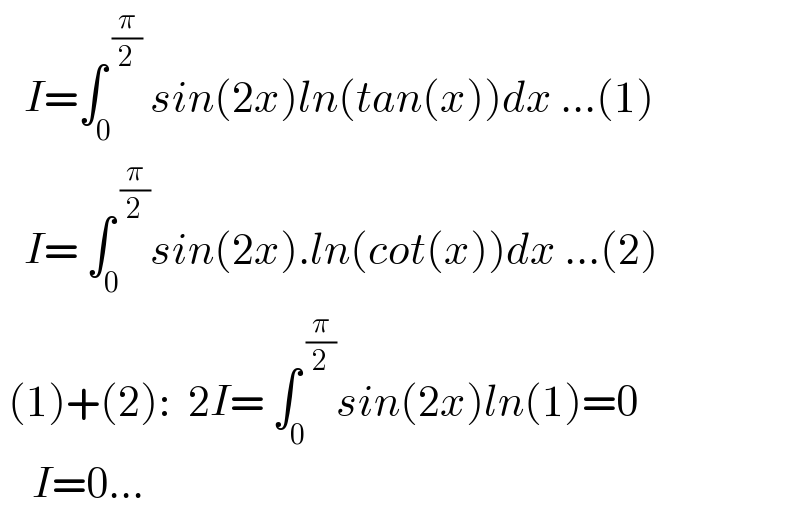
$$\:\:\:{I}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:{sin}\left(\mathrm{2}{x}\right){ln}\left({tan}\left({x}\right)\right){dx}\:…\left(\mathrm{1}\right) \\ $$$$\:\:\:{I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left(\mathrm{2}{x}\right).{ln}\left({cot}\left({x}\right)\right){dx}\:…\left(\mathrm{2}\right) \\ $$$$\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right):\:\:\mathrm{2}{I}=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}\left(\mathrm{2}{x}\right){ln}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:\:\:{I}=\mathrm{0}… \\ $$
