Question Number 1873 by 123456 last updated on 19/Oct/15
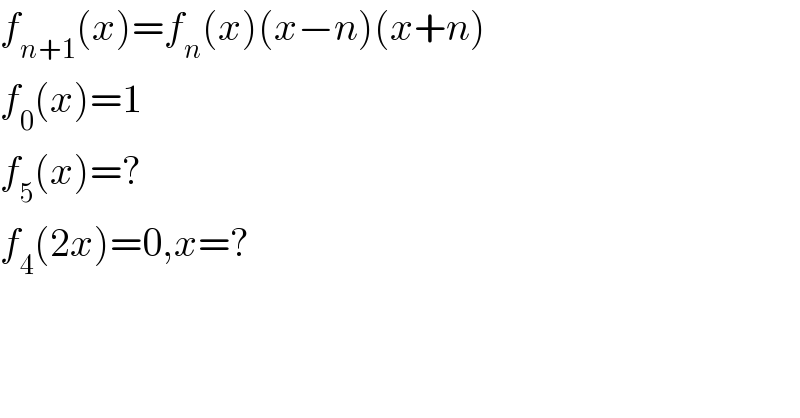
$${f}_{{n}+\mathrm{1}} \left({x}\right)={f}_{{n}} \left({x}\right)\left({x}−{n}\right)\left({x}+{n}\right) \\ $$$${f}_{\mathrm{0}} \left({x}\right)=\mathrm{1} \\ $$$${f}_{\mathrm{5}} \left({x}\right)=? \\ $$$${f}_{\mathrm{4}} \left(\mathrm{2}{x}\right)=\mathrm{0},{x}=? \\ $$
Answered by Rasheed Soomro last updated on 19/Oct/15
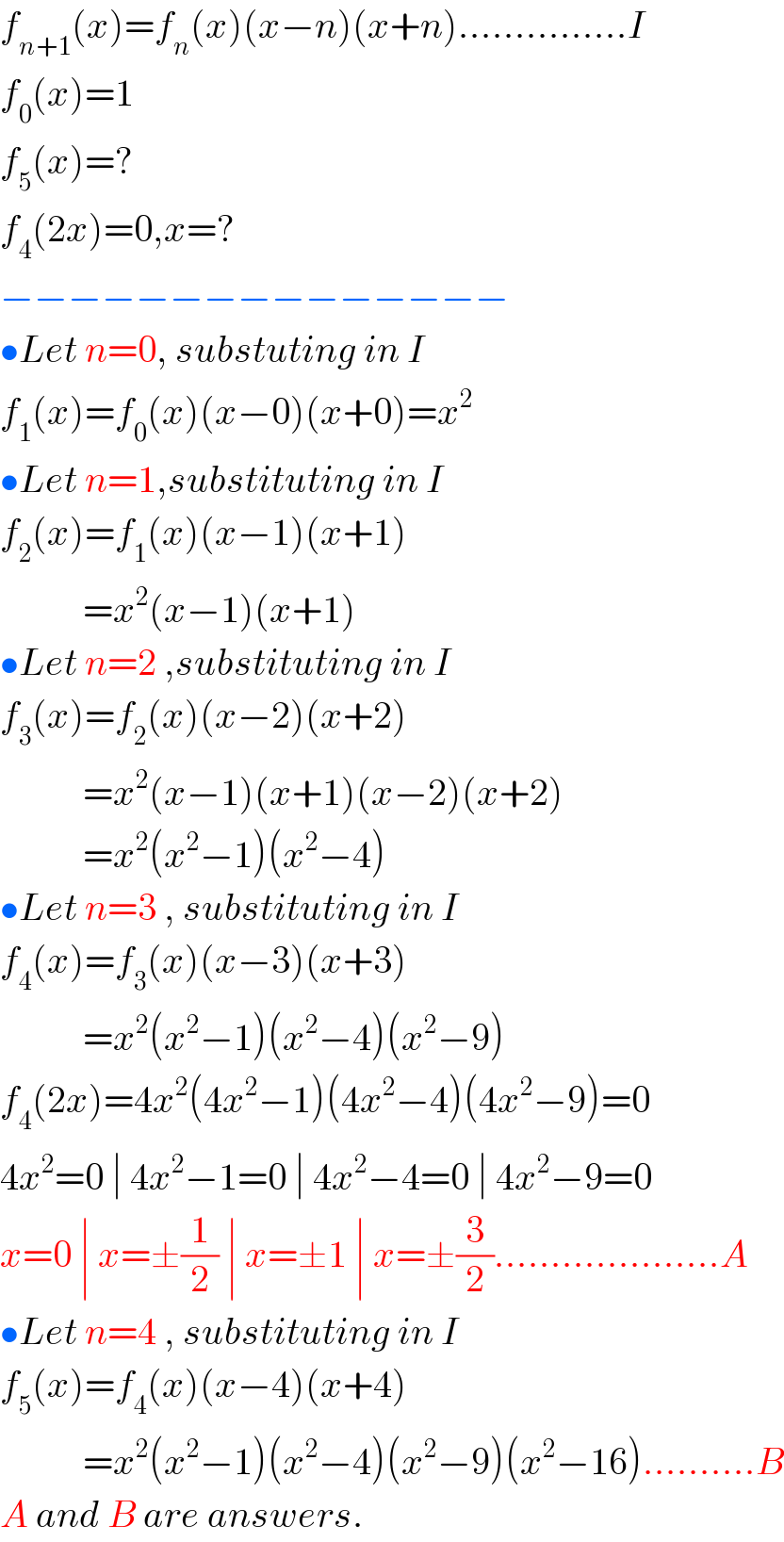
$${f}_{{n}+\mathrm{1}} \left({x}\right)={f}_{{n}} \left({x}\right)\left({x}−{n}\right)\left({x}+{n}\right)……………{I} \\ $$$${f}_{\mathrm{0}} \left({x}\right)=\mathrm{1} \\ $$$${f}_{\mathrm{5}} \left({x}\right)=? \\ $$$${f}_{\mathrm{4}} \left(\mathrm{2}{x}\right)=\mathrm{0},{x}=? \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\bullet{Let}\:{n}=\mathrm{0},\:{substuting}\:{in}\:{I} \\ $$$${f}_{\mathrm{1}} \left({x}\right)={f}_{\mathrm{0}} \left({x}\right)\left({x}−\mathrm{0}\right)\left({x}+\mathrm{0}\right)={x}^{\mathrm{2}} \\ $$$$\bullet{Let}\:{n}=\mathrm{1},{substituting}\:{in}\:{I} \\ $$$${f}_{\mathrm{2}} \left({x}\right)={f}_{\mathrm{1}} \left({x}\right)\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right) \\ $$$$\bullet{Let}\:{n}=\mathrm{2}\:,{substituting}\:{in}\:{I} \\ $$$${f}_{\mathrm{3}} \left({x}\right)={f}_{\mathrm{2}} \left({x}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$$\bullet{Let}\:{n}=\mathrm{3}\:,\:{substituting}\:{in}\:{I} \\ $$$${f}_{\mathrm{4}} \left({x}\right)={f}_{\mathrm{3}} \left({x}\right)\left({x}−\mathrm{3}\right)\left({x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{4}\right)\left({x}^{\mathrm{2}} −\mathrm{9}\right) \\ $$$${f}_{\mathrm{4}} \left(\mathrm{2}{x}\right)=\mathrm{4}{x}^{\mathrm{2}} \left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}\right)=\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} =\mathrm{0}\:\mid\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\mid\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}\:\mid\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{9}=\mathrm{0} \\ $$$${x}=\mathrm{0}\:\mid\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\:\mid\:{x}=\pm\mathrm{1}\:\mid\:{x}=\pm\frac{\mathrm{3}}{\mathrm{2}}………………..{A} \\ $$$$\bullet{Let}\:{n}=\mathrm{4}\:,\:{substituting}\:{in}\:{I}\: \\ $$$${f}_{\mathrm{5}} \left({x}\right)={f}_{\mathrm{4}} \left({x}\right)\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{4}\right)\left({x}^{\mathrm{2}} −\mathrm{9}\right)\left({x}^{\mathrm{2}} −\mathrm{16}\right)……….{B} \\ $$$${A}\:{and}\:{B}\:{are}\:{answers}. \\ $$
