Question Number 67431 by aliesam last updated on 27/Aug/19
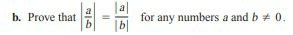
Commented by mathmax by abdo last updated on 27/Aug/19
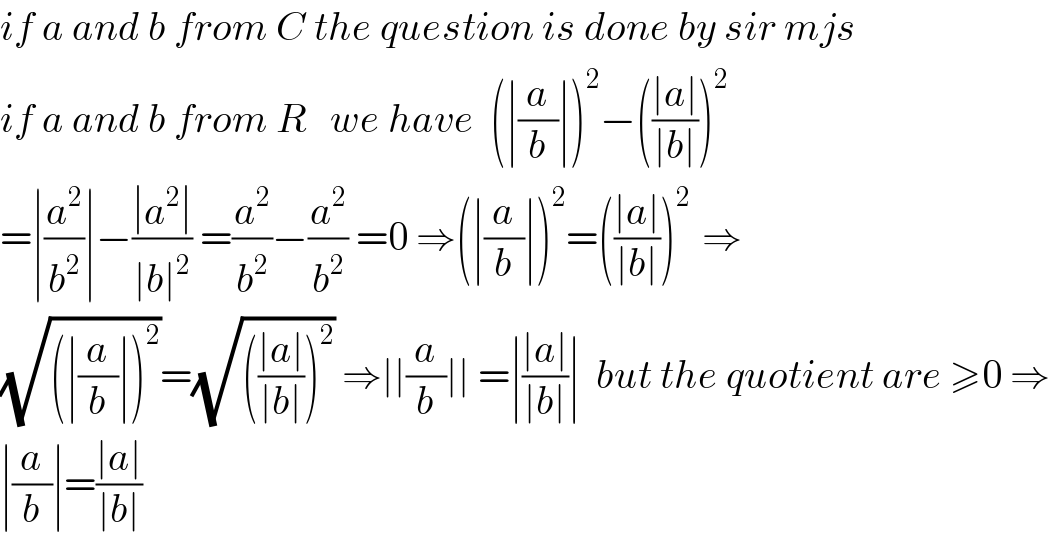
$${if}\:{a}\:{and}\:{b}\:{from}\:{C}\:{the}\:{question}\:{is}\:{done}\:{by}\:{sir}\:{mjs} \\ $$$${if}\:{a}\:{and}\:{b}\:{from}\:{R}\:\:\:{we}\:{have}\:\:\left(\mid\frac{{a}}{{b}}\mid\right)^{\mathrm{2}} −\left(\frac{\mid{a}\mid}{\mid{b}\mid}\right)^{\mathrm{2}} \: \\ $$$$=\mid\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\mid−\frac{\mid{a}^{\mathrm{2}} \mid}{\mid{b}\mid^{\mathrm{2}} }\:=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\mathrm{0}\:\Rightarrow\left(\mid\frac{{a}}{{b}}\mid\right)^{\mathrm{2}} =\left(\frac{\mid{a}\mid}{\mid{b}\mid}\right)^{\mathrm{2}\:} \:\Rightarrow \\ $$$$\sqrt{\left(\mid\frac{{a}}{{b}}\mid\right)^{\mathrm{2}} }=\sqrt{\left(\frac{\mid{a}\mid}{\mid{b}\mid}\right)^{\mathrm{2}} }\:\Rightarrow\mid\mid\frac{{a}}{{b}}\mid\mid\:=\mid\frac{\mid{a}\mid}{\mid{b}\mid}\mid\:\:{but}\:{the}\:{quotient}\:{are}\:\geqslant\mathrm{0}\:\Rightarrow \\ $$$$\mid\frac{{a}}{{b}}\mid=\frac{\mid{a}\mid}{\mid{b}\mid} \\ $$
Answered by MJS last updated on 27/Aug/19
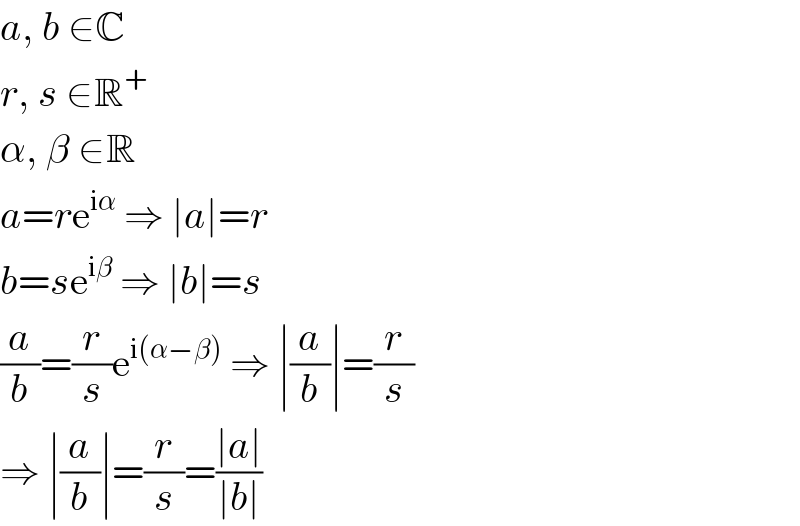
$${a},\:{b}\:\in\mathbb{C} \\ $$$${r},\:{s}\:\in\mathbb{R}^{+} \\ $$$$\alpha,\:\beta\:\in\mathbb{R} \\ $$$${a}={r}\mathrm{e}^{\mathrm{i}\alpha} \:\Rightarrow\:\mid{a}\mid={r} \\ $$$${b}={s}\mathrm{e}^{\mathrm{i}\beta} \:\Rightarrow\:\mid{b}\mid={s} \\ $$$$\frac{{a}}{{b}}=\frac{{r}}{{s}}\mathrm{e}^{\mathrm{i}\left(\alpha−\beta\right)} \:\Rightarrow\:\mid\frac{{a}}{{b}}\mid=\frac{{r}}{{s}} \\ $$$$\Rightarrow\:\mid\frac{{a}}{{b}}\mid=\frac{{r}}{{s}}=\frac{\mid{a}\mid}{\mid{b}\mid} \\ $$
