Menu Close

x-4-c-3-x-3-c-2-x-2-c-1-x-c-0-0-for-c-n-R-this-can-have-4-unique-zeros-R-2-unique-zeros-1-double-zero-R-2-double-zeros-R-1-triple-1-unique-zeros-R-1-fourfold-zero-R-2-unique-zeros-R-1

Tinku Tara 0 Comments
Pin




Question Number 152625 by Dandelion last updated on 30/Aug/21
x^4 +c_3 x^3 +c_2 x^2 +c_1 x+c_0 =0 for c_n ∈R this can have 4 unique zeros ∈R 2 unique zeros + 1 double zero ∈R 2 double zeros ∈R 1 triple + 1 unique zeros ∈R 1 fourfold zero ∈R 2 unique zeros ∈R + 1 pair of complex zeros 1 double zero ∈R + 1 pair of complex zeros 2 pairs of complex zeros 2 double imaginary zeros for given c_n ; can we decide which case we have without solving?
$${x}^{\mathrm{4}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{for}\:{c}_{{n}} \in\mathbb{R}\:\mathrm{this}\:\mathrm{can}\:\mathrm{have} \\ $$$$\mathrm{4}\:\mathrm{unique}\:\mathrm{zeros}\:\in\mathbb{R} \\ $$$$\mathrm{2}\:\mathrm{unique}\:\mathrm{zeros}\:+\:\mathrm{1}\:\mathrm{double}\:\mathrm{zero}\:\in\mathbb{R} \\ $$$$\mathrm{2}\:\mathrm{double}\:\mathrm{zeros}\:\in\mathbb{R} \\ $$$$\mathrm{1}\:\mathrm{triple}\:+\:\mathrm{1}\:\mathrm{unique}\:\mathrm{zeros}\:\in\mathbb{R} \\ $$$$\mathrm{1}\:\mathrm{fourfold}\:\mathrm{zero}\:\in\mathbb{R} \\ $$$$\mathrm{2}\:\mathrm{unique}\:\mathrm{zeros}\:\in\mathbb{R}\:+\:\mathrm{1}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{zeros} \\ $$$$\mathrm{1}\:\mathrm{double}\:\mathrm{zero}\:\in\mathbb{R}\:+\:\mathrm{1}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{zeros} \\ $$$$\mathrm{2}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{complex}\:\mathrm{zeros} \\ $$$$\mathrm{2}\:\mathrm{double}\:\mathrm{imaginary}\:\mathrm{zeros} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{given}\:{c}_{{n}} ;\:\mathrm{can}\:\mathrm{we}\:\mathrm{decide}\:\mathrm{which}\:\mathrm{case}\:\mathrm{we} \\ $$$$\mathrm{have}\:\mathrm{without}\:\mathrm{solving}? \\ $$
Commented by Dandelion last updated on 30/Aug/21
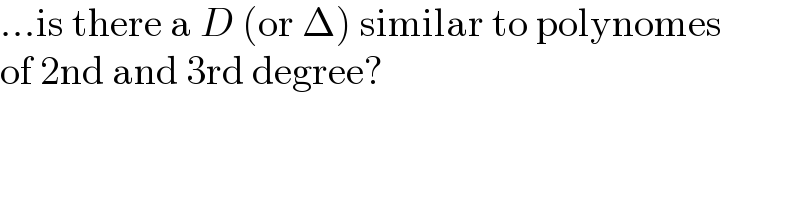
...is there a D (or Δ) similar to polynomes of 2nd and 3rd degree?
$$…\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:{D}\:\left(\mathrm{or}\:\Delta\right)\:\mathrm{similar}\:\mathrm{to}\:\mathrm{polynomes} \\ $$$$\mathrm{of}\:\mathrm{2nd}\:\mathrm{and}\:\mathrm{3rd}\:\mathrm{degree}? \\ $$
Commented by MJS_new last updated on 31/Aug/21
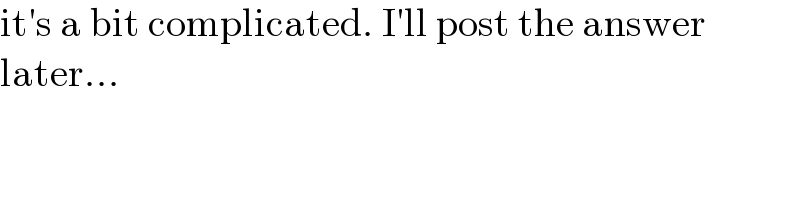
it′s a bit complicated. I′ll post the answer later...
$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{bit}\:\mathrm{complicated}.\:\mathrm{I}'\mathrm{ll}\:\mathrm{post}\:\mathrm{the}\:\mathrm{answer} \\ $$$$\mathrm{later}… \\ $$
Answered by MJS_new last updated on 02/Sep/21
x^4 +c_3 x^3 +c_2 x^2 +c_1 x+c_0 =0 1. let x=t−(c_3 /4) and rename the new constants ⇒ t^4 +pt^2 +qt+r=0 D_1 =16p^4 r−4p^3 q^2 −128p^2 r^2 +144pq^2 r−27q^4 +256r^3 D_2 =p^2 +12r D_3 =−p^2 +4r (1) D_1 <0 ⇒ 2 unique real + 1 pair of conjugated complex solutions (2) D_1 >0∧p<0∧D_3 <0 ⇒ 4 unique real solutions (3) D_1 >0∧(p>0∨D_3 >0) ⇒ 2 pairs of conjugated complex solutions (4) D_1 =0∧p<0∧D_3 <0∧D_2 ≠0 ⇒ 1 real double + 2 unique real solutions (5) D_1 =0∧(D_3 >0∨p>0∧(D_3 ≠0∨q≠0)) ⇒ 1 real double + 1 pair of conjugated complex solutions (6) D_1 =0∧D_2 =0∧D_3 ≠0 ⇒ 1 real triple + 1 unique real solutions (7) D_1 =0∧D_3 =0∧p<0 ⇒ 2 real double solutions (8) D_1 =0∧D_3 =0∧p>0∧q=0 ⇒ 2 imaginary double solutions (9) D_1 =0∧D_2 =0 ⇒ 1 real fourfold solution
$${x}^{\mathrm{4}} +{c}_{\mathrm{3}} {x}^{\mathrm{3}} +{c}_{\mathrm{2}} {x}^{\mathrm{2}} +{c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} =\mathrm{0} \\ $$$$\mathrm{1}.\:\mathrm{let}\:{x}={t}−\frac{{c}_{\mathrm{3}} }{\mathrm{4}}\:\mathrm{and}\:\mathrm{rename}\:\mathrm{the}\:\mathrm{new}\:\mathrm{constants} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{4}} +{pt}^{\mathrm{2}} +{qt}+{r}=\mathrm{0} \\ $$$$ \\ $$$${D}_{\mathrm{1}} =\mathrm{16}{p}^{\mathrm{4}} {r}−\mathrm{4}{p}^{\mathrm{3}} {q}^{\mathrm{2}} −\mathrm{128}{p}^{\mathrm{2}} {r}^{\mathrm{2}} +\mathrm{144}{pq}^{\mathrm{2}} {r}−\mathrm{27}{q}^{\mathrm{4}} +\mathrm{256}{r}^{\mathrm{3}} \\ $$$${D}_{\mathrm{2}} ={p}^{\mathrm{2}} +\mathrm{12}{r} \\ $$$${D}_{\mathrm{3}} =−{p}^{\mathrm{2}} +\mathrm{4}{r} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{D}_{\mathrm{1}} <\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{unique}\:\mathrm{real}\:+\:\mathrm{1}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{conjugated}\:\mathrm{complex}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:{D}_{\mathrm{1}} >\mathrm{0}\wedge{p}<\mathrm{0}\wedge{D}_{\mathrm{3}} <\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{4}\:\mathrm{unique}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:{D}_{\mathrm{1}} >\mathrm{0}\wedge\left({p}>\mathrm{0}\vee{D}_{\mathrm{3}} >\mathrm{0}\right) \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{conjugated}\:\mathrm{complex}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{4}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge{p}<\mathrm{0}\wedge{D}_{\mathrm{3}} <\mathrm{0}\wedge{D}_{\mathrm{2}} \neq\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{double}\:+\:\mathrm{2}\:\mathrm{unique}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{5}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge\left({D}_{\mathrm{3}} >\mathrm{0}\vee{p}>\mathrm{0}\wedge\left({D}_{\mathrm{3}} \neq\mathrm{0}\vee{q}\neq\mathrm{0}\right)\right) \\ $$$$\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{double}\:+\:\mathrm{1}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{conjugated}\:\mathrm{complex}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{6}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge{D}_{\mathrm{2}} =\mathrm{0}\wedge{D}_{\mathrm{3}} \neq\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{triple}\:+\:\mathrm{1}\:\mathrm{unique}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{7}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge{D}_{\mathrm{3}} =\mathrm{0}\wedge{p}<\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{real}\:\mathrm{double}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{8}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge{D}_{\mathrm{3}} =\mathrm{0}\wedge{p}>\mathrm{0}\wedge{q}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}\:\mathrm{imaginary}\:\mathrm{double}\:\mathrm{solutions} \\ $$$$ \\ $$$$\left(\mathrm{9}\right)\:{D}_{\mathrm{1}} =\mathrm{0}\wedge{D}_{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{1}\:\mathrm{real}\:\mathrm{fourfold}\:\mathrm{solution} \\ $$
Commented by Tawa11 last updated on 02/Sep/21
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *