Question Number 133004 by liberty last updated on 18/Feb/21

$$\mathrm{If}\:\int\:\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=\:\mathrm{x}−\frac{{k}}{\:\sqrt{{A}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{{k}\:\mathrm{tan}\:{x}+\mathrm{1}}{\:\sqrt{{A}}}\right)+\mathrm{C} \\ $$$$\mathrm{where}\:\mathrm{C}\:\mathrm{is}\:\mathrm{constant}\:\mathrm{of}\:\mathrm{integration}. \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{ordered}\:\mathrm{pair}\:\left({k},\mathrm{A}\right)\:\mathrm{is}\: \\ $$$$\mathrm{equal}\:\mathrm{to}\: \\ $$
Answered by EDWIN88 last updated on 18/Feb/21
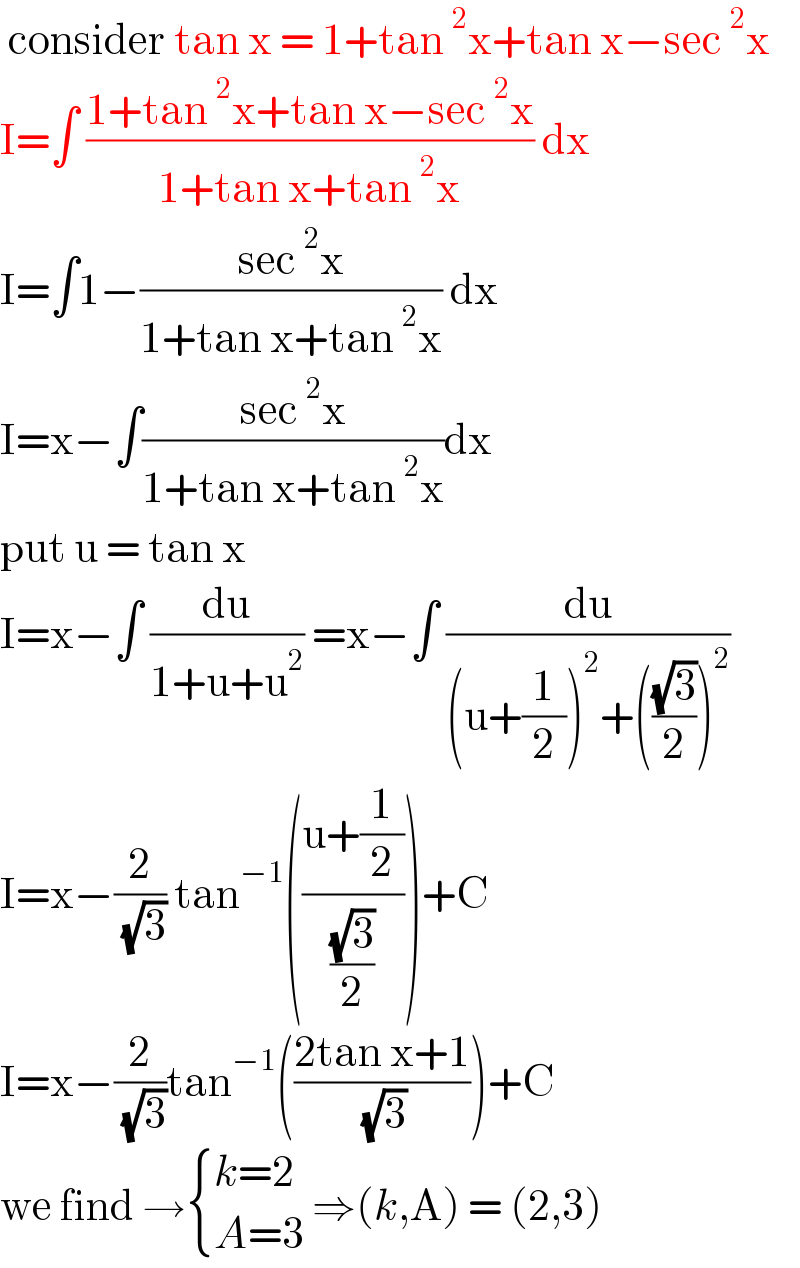
$$\:\mathrm{consider}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:\mathrm{x}−\mathrm{sec}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}+\mathrm{tan}\:\mathrm{x}−\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{I}=\int\mathrm{1}−\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{I}=\mathrm{x}−\int\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}+\mathrm{tan}\:\mathrm{x}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{put}\:\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{x}\: \\ $$$$\mathrm{I}=\mathrm{x}−\int\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}+\mathrm{u}^{\mathrm{2}} }\:=\mathrm{x}−\int\:\frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}=\mathrm{x}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+\mathrm{C} \\ $$$$\mathrm{I}=\mathrm{x}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2tan}\:\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{C}\: \\ $$$$\mathrm{we}\:\mathrm{find}\:\rightarrow\begin{cases}{{k}=\mathrm{2}}\\{{A}=\mathrm{3}}\end{cases}\:\Rightarrow\left({k},\mathrm{A}\right)\:=\:\left(\mathrm{2},\mathrm{3}\right) \\ $$
