Menu Close

i-still-search-about-a-general-and-complete-solution-about-this-determine-x-in-N-where-7-divise-2-x-3-x-note-it-is-just-an-exercise-in-secondary-so-dont-go-away-maybe-we-must-use-separation-of

Tinku Tara 0 Comments
Pin




Question Number 21990 by hi147 last updated on 08/Oct/17
i still search about a general and complete solution about this determine x in N where 7 divise 2^x +3^x note = it is just an exercise in secondary so dont go away... maybe we must use separation of cases methode....
$${i}\:{still}\:{search}\:{about}\:{a}\:{general}\:{and}\: \\ $$$${complete}\:{solution}\:{about}\:{this} \\ $$$${determine}\:{x}\:{in}\:{N}\:{where}\:\mathrm{7}\:{divise}\:\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \\ $$$${note}\:=\:{it}\:{is}\:{just}\:{an}\:{exercise}\:{in}\:{secondary} \\ $$$${so}\:{dont}\:{go}\:{away}… \\ $$$${maybe}\:{we}\:{must}\:{use}\:{separation}\:{of}\:{cases} \\ $$$${methode}…. \\ $$
Commented by Tinkutara last updated on 11/Oct/17
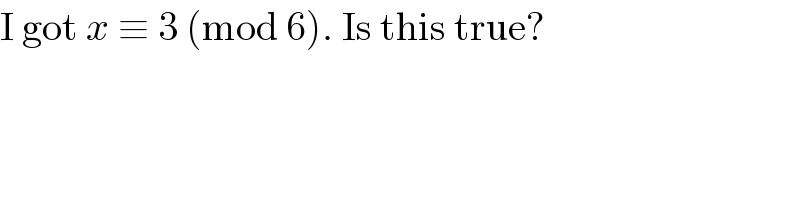
I got x ≡ 3 (mod 6). Is this true?
$$\mathrm{I}\:\mathrm{got}\:{x}\:\equiv\:\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{6}\right).\:\mathrm{Is}\:\mathrm{this}\:\mathrm{true}? \\ $$
Answered by Tinkutara last updated on 11/Oct/17
By Fermat′s little theorem, 2^6 ≡1(mod 7) ⇒2^(6k+r) ≡2^r (mod 7) Similarly, 3^(6k+r) ≡3^r (mod 7) ⇒ 2^(6k+r) +3^(6k+r) ≡2^r +3^r (mod 7) For k=0 and trying for 0<r<6, 2^1 +3^1 ≡5(mod 7) 2^2 +3^2 ≡6(mod 7) 2^3 +3^3 ≡0(mod 7) 2^4 +3^4 ≡6(mod 7) 2^1 +3^1 ≡2(mod 7) Hence x≡3(mod 6).
$${By}\:{Fermat}'{s}\:{little}\:{theorem}, \\ $$$$\mathrm{2}^{\mathrm{6}} \equiv\mathrm{1}\left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{6}{k}+{r}} \equiv\mathrm{2}^{{r}} \left({mod}\:\mathrm{7}\right) \\ $$$${Similarly},\:\mathrm{3}^{\mathrm{6}{k}+{r}} \equiv\mathrm{3}^{{r}} \left({mod}\:\mathrm{7}\right) \\ $$$$\Rightarrow\:\mathrm{2}^{\mathrm{6}{k}+{r}} +\mathrm{3}^{\mathrm{6}{k}+{r}} \equiv\mathrm{2}^{{r}} +\mathrm{3}^{{r}} \left({mod}\:\mathrm{7}\right) \\ $$$${For}\:{k}=\mathrm{0}\:{and}\:{trying}\:{for}\:\mathrm{0}<{r}<\mathrm{6}, \\ $$$$\mathrm{2}^{\mathrm{1}} +\mathrm{3}^{\mathrm{1}} \equiv\mathrm{5}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \equiv\mathrm{6}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} \equiv\mathrm{0}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}^{\mathrm{4}} +\mathrm{3}^{\mathrm{4}} \equiv\mathrm{6}\left({mod}\:\mathrm{7}\right) \\ $$$$\mathrm{2}^{\mathrm{1}} +\mathrm{3}^{\mathrm{1}} \equiv\mathrm{2}\left({mod}\:\mathrm{7}\right) \\ $$$${Hence}\:{x}\equiv\mathrm{3}\left({mod}\:\mathrm{6}\right). \\ $$
Commented by hi147 last updated on 16/Oct/17
thats good but how can we prove that it is the only solution.i mean 6k+3. and we have an other problem = it is just an exercise in secondary and we dont have fermat s littel theorem in this livel.so.....
$${thats}\:{good}\:{but}\:{how}\:{can}\:{we}\:{prove}\:{that} \\ $$$${it}\:{is}\:{the}\:{only}\:{solution}.{i}\:{mean}\:\mathrm{6}{k}+\mathrm{3}.\: \\ $$$${and}\:{we}\:{have}\:{an}\:{other}\:{problem}\:=\:{it}\:{is} \\ $$$${just}\:{an}\:{exercise}\:{in}\:{secondary} \\ $$$${and}\:{we}\:{dont}\:{have}\:{fermat}\:{s}\:{littel}\:{theorem} \\ $$$${in}\:{this}\:{livel}.{so}….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *