Question Number 87757 by john santu last updated on 06/Apr/20
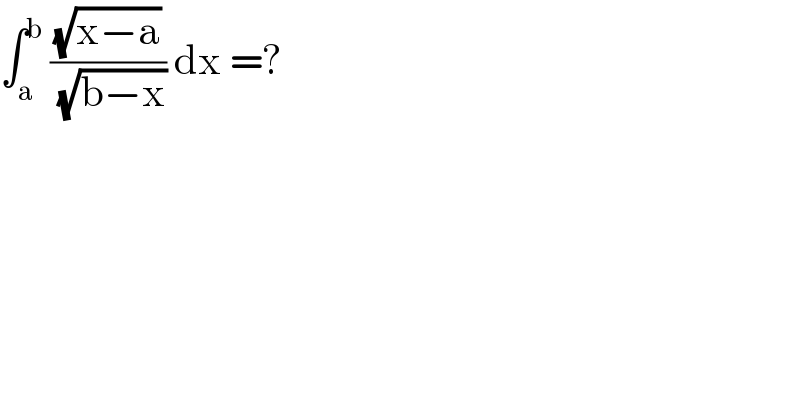
$$\int_{\mathrm{a}} ^{\mathrm{b}} \:\frac{\sqrt{\mathrm{x}−\mathrm{a}}}{\:\sqrt{\mathrm{b}−\mathrm{x}}}\:\mathrm{dx}\:=?\: \\ $$
Commented by john santu last updated on 06/Apr/20
![let x = a + (b−a) w ] x = a ⇒ w = 0 x = b ⇒ w = 1 ∫ _0 ^( 1) ((√((b−a)w))/( (√((b−a)(1−w))))) (b−a) dw = ∫_0 ^1 (b−a) ((√w)/( (√(1−w)))) dw = [ let (√w) = sin t ] (b−a) ∫ _0 ^(π/2) ((sin t)/(cos t)) × 2sin t cos t dt = (b−a) ∫_0 ^(π/2) 2sin^2 t dt = (b−a) ∫ _0 ^(π/2) (1−cos 2t) dt = (b−a) [ t − (1/2)sin 2t ]^(π/2) _( 0) = ((π(b−a))/2)](https://www.tinkutara.com/question/Q87758.png)
$$\left.\mathrm{let}\:\mathrm{x}\:=\:\mathrm{a}\:+\:\left(\mathrm{b}−\mathrm{a}\right)\:\mathrm{w}\:\right] \\ $$$$\mathrm{x}\:=\:\mathrm{a}\:\Rightarrow\:\mathrm{w}\:=\:\mathrm{0} \\ $$$$\mathrm{x}\:=\:\mathrm{b}\:\Rightarrow\:\mathrm{w}\:=\:\mathrm{1} \\ $$$$\int\underset{\mathrm{0}} {\overset{\:\mathrm{1}} {\:}}\:\frac{\sqrt{\left(\mathrm{b}−\mathrm{a}\right)\mathrm{w}}}{\:\sqrt{\left(\mathrm{b}−\mathrm{a}\right)\left(\mathrm{1}−\mathrm{w}\right)}}\:\left(\mathrm{b}−\mathrm{a}\right)\:\mathrm{dw}\:= \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{b}−\mathrm{a}\right)\:\frac{\sqrt{\mathrm{w}}}{\:\sqrt{\mathrm{1}−\mathrm{w}}}\:\mathrm{dw}\:= \\ $$$$\left[\:\mathrm{let}\:\sqrt{\mathrm{w}}\:=\:\mathrm{sin}\:\mathrm{t}\:\right]\: \\ $$$$\left(\mathrm{b}−\mathrm{a}\right)\:\int\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\:}}\:\frac{\mathrm{sin}\:\mathrm{t}}{\mathrm{cos}\:\mathrm{t}}\:×\:\mathrm{2sin}\:\mathrm{t}\:\mathrm{cos}\:\mathrm{t}\:\mathrm{dt}\:= \\ $$$$\left(\mathrm{b}−\mathrm{a}\right)\:\underset{\mathrm{0}} {\int}\overset{\frac{\pi}{\mathrm{2}}} {\:}\:\mathrm{2sin}\:^{\mathrm{2}} \:\mathrm{t}\:\mathrm{dt}\:= \\ $$$$\left(\mathrm{b}−\mathrm{a}\right)\:\int\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\:}}\:\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2t}\right)\:\mathrm{dt}\:= \\ $$$$\left(\mathrm{b}−\mathrm{a}\right)\:\left[\:\mathrm{t}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2t}\:\underset{\:\:\:\mathrm{0}} {\right]}^{\frac{\pi}{\mathrm{2}}} = \\ $$$$\frac{\pi\left(\mathrm{b}−\mathrm{a}\right)}{\mathrm{2}} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 06/Apr/20
![I=∫_a ^b ((√(x−a))/( (√(b−x)))) dx ⇒I =∫_a ^b (√((x−a)/(b−x)))dx we do the changrmrnt (√((x−a)/(b−x)))=t ⇒((x−a)/(b−x))=t^2 ⇒x−a=bt^2 −t^2 x ⇒ (1+t^2 )x =bt^2 +a ⇒x =((bt^2 +a)/(t^2 +1)) ⇒ (dx/dt) =((2bt(t^2 +1)−2t(bt^2 +a))/((t^2 +1)^2 )) =((2bt−2at)/((t^2 +1)^2 )) ⇒ I =(2b−2a)∫_0 ^(+∞) (t^2 /((t^2 +1)^2 ))dt =(2b−2a)∫_0 ^∞ ((t^2 +1−1)/((t^2 +1)^2 ))dt =(2b−2a)∫_0 ^∞ (dt/(1+t^2 )) −(2b−2a)∫_0 ^∞ (dt/((t^2 +1)^2 )) =π(b−a)−(2b−2a)∫_0 ^∞ (dt/((t^2 +1)^2 )) we have ∫_0 ^∞ (dt/((t^2 +1)^2 )) =_(t=tsnθ) ∫_0 ^(π/2) ((1+tan^2 θ)/((1+tan^2 θ)^2 ))dθ =∫_0 ^(π/2) (dθ/(1+tan^2 θ)) =∫_0 ^(π/2) ((1+cos(2θ))/2) =(π/4) +(1/4)[sin(2θ)]_0 ^(π/2) =(π/4) ⇒ I =π(b−a)−(((b−a)π)/2) ⇒ I =(π/2)(b−a)](https://www.tinkutara.com/question/Q87761.png)
$${I}=\int_{{a}} ^{{b}} \:\frac{\sqrt{{x}−{a}}}{\:\sqrt{{b}−{x}}}\:{dx}\:\:\Rightarrow{I}\:=\int_{{a}} ^{{b}} \sqrt{\frac{{x}−{a}}{{b}−{x}}}{dx}\:{we}\:{do}\:{the}\:{changrmrnt} \\ $$$$\sqrt{\frac{{x}−{a}}{{b}−{x}}}={t}\:\Rightarrow\frac{{x}−{a}}{{b}−{x}}={t}^{\mathrm{2}} \:\Rightarrow{x}−{a}={bt}^{\mathrm{2}} −{t}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$$\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}\:={bt}^{\mathrm{2}} \:+{a}\:\Rightarrow{x}\:=\frac{{bt}^{\mathrm{2}} \:+{a}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:\:=\frac{\mathrm{2}{bt}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2}{t}\left({bt}^{\mathrm{2}} \:+{a}\right)}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{bt}−\mathrm{2}{at}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int_{\mathrm{0}} ^{+\infty} \:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\pi\left({b}−{a}\right)−\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=_{{t}={tsn}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\pi\left({b}−{a}\right)−\frac{\left({b}−{a}\right)\pi}{\mathrm{2}}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\left({b}−{a}\right) \\ $$$$ \\ $$
