Question Number 22365 by A1B1C1D1 last updated on 16/Oct/17

Answered by sma3l2996 last updated on 16/Oct/17

$$=\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\frac{\mathrm{1}}{\mathrm{5}^{{x}} }}{\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\frac{\mathrm{1}}{\mathrm{5}^{{x}} {x}}}=\frac{\mathrm{1}−\mathrm{0}+\mathrm{0}}{\mathrm{1}+\mathrm{0}+\mathrm{0}}=\mathrm{1}\:\: \\ $$
Commented by A1B1C1D1 last updated on 16/Oct/17
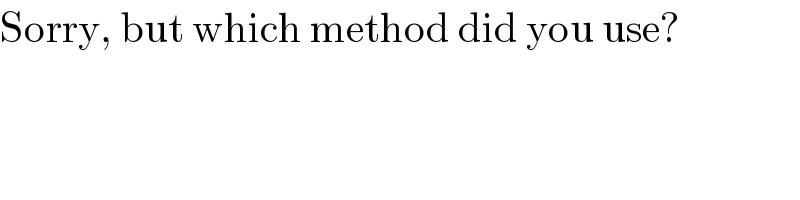
$$\mathrm{Sorry},\:\mathrm{but}\:\mathrm{which}\:\mathrm{method}\:\mathrm{did}\:\mathrm{you}\:\mathrm{use}? \\ $$
Commented by sma3l2996 last updated on 16/Oct/17
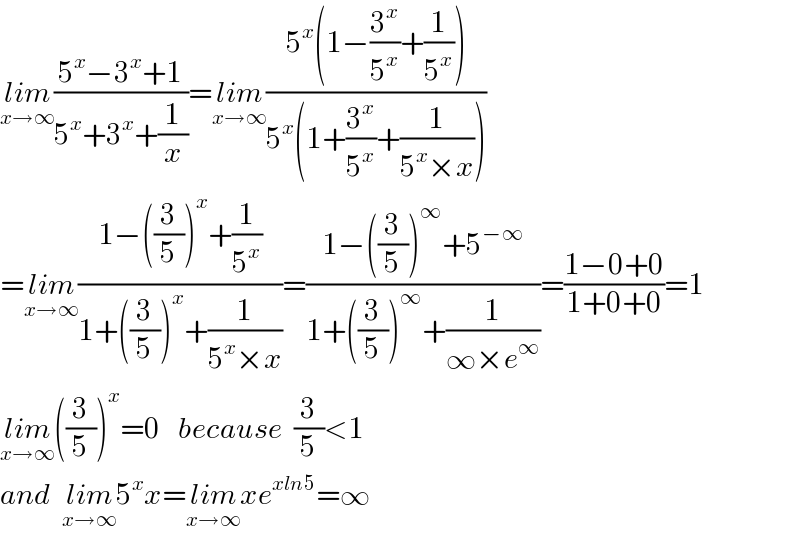
$$\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{5}^{{x}} −\mathrm{3}^{{x}} +\mathrm{1}}{\mathrm{5}^{{x}} +\mathrm{3}^{{x}} +\frac{\mathrm{1}}{{x}}}=\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{5}^{{x}} \left(\mathrm{1}−\frac{\mathrm{3}^{{x}} }{\mathrm{5}^{{x}} }+\frac{\mathrm{1}}{\mathrm{5}^{{x}} }\right)}{\mathrm{5}^{{x}} \left(\mathrm{1}+\frac{\mathrm{3}^{{x}} }{\mathrm{5}^{{x}} }+\frac{\mathrm{1}}{\mathrm{5}^{{x}} ×{x}}\right)} \\ $$$$=\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\frac{\mathrm{1}}{\mathrm{5}^{{x}} }}{\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\frac{\mathrm{1}}{\mathrm{5}^{{x}} ×{x}}}=\frac{\mathrm{1}−\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\infty} +\mathrm{5}^{−\infty} }{\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\infty} +\frac{\mathrm{1}}{\infty×{e}^{\infty} }}=\frac{\mathrm{1}−\mathrm{0}+\mathrm{0}}{\mathrm{1}+\mathrm{0}+\mathrm{0}}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\infty} {{lim}}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} =\mathrm{0}\:\:\:{because}\:\:\frac{\mathrm{3}}{\mathrm{5}}<\mathrm{1} \\ $$$${and}\:\:\underset{{x}\rightarrow\infty} {{lim}}\mathrm{5}^{{x}} {x}=\underset{{x}\rightarrow\infty} {{lim}xe}^{{xln}\mathrm{5}} =\infty \\ $$
