Question-153464

Question Number 153464 by roxceefocus last updated on 07/Sep/21

Commented by roxceefocus last updated on 07/Sep/21

$${pls}\:{i}\:{need}\:{answers}\:{on}\:{this}\:{question} \\ $$

Answered by Rasheed.Sindhi last updated on 07/Sep/21

(√(3x+1))−(√(2x−1))=1 ( (√(3x+1))−(√(2x−1))=1 )^2 3x+1+2x−1−2(√((3x+1)(2x−1))=1 ( 5x−1=2(√((3x+1)(2x−1))) )^2 (5x−1)^2 =4(3x+1)(2x−1) 25x^2 −10x+1=4(6x^2 −3x+2x−1) 25x^2 −10x+1=24x^2 −4x−4 x^2 −6x+5=0 (x−1)(x−5)=0 x=1 ∣ x=5 On verification we can see that both roots satisfy the original eqn

$$\sqrt{\mathrm{3}{x}+\mathrm{1}}−\sqrt{\mathrm{2}{x}−\mathrm{1}}=\mathrm{1} \\ $$$$\left(\:\sqrt{\mathrm{3}{x}+\mathrm{1}}−\sqrt{\mathrm{2}{x}−\mathrm{1}}=\mathrm{1}\:\right)^{\mathrm{2}} \\ $$$$\mathrm{3}{x}+\mathrm{1}+\mathrm{2}{x}−\mathrm{1}−\mathrm{2}\sqrt{\left(\mathrm{3}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right.}=\mathrm{1} \\ $$$$\left(\:\mathrm{5}{x}−\mathrm{1}=\mathrm{2}\sqrt{\left(\mathrm{3}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)}\:\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{5}{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{3}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right) \\ $$$$\mathrm{25}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{1}=\mathrm{4}\left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}{x}−\mathrm{1}\right) \\ $$$$\mathrm{25}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{1}=\mathrm{24}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{4} \\ $$$${x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1}\:\mid\:{x}=\mathrm{5} \\ $$$${On}\:{verification}\:{we}\:{can}\:{see}\:{that} \\ $$$${both}\:{roots}\:{satisfy}\:{the}\:{original}\:{eqn} \\ $$

Answered by puissant last updated on 07/Sep/21

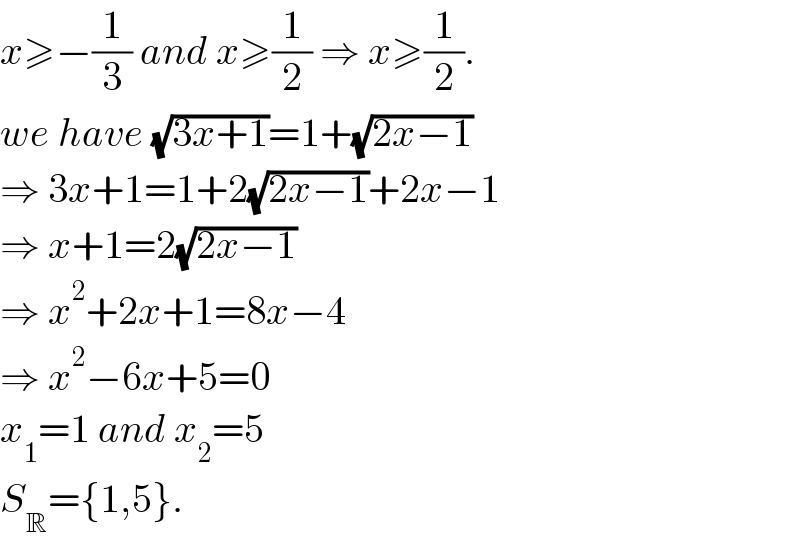
x≥−(1/3) and x≥(1/2) ⇒ x≥(1/2). we have (√(3x+1))=1+(√(2x−1)) ⇒ 3x+1=1+2(√(2x−1))+2x−1 ⇒ x+1=2(√(2x−1)) ⇒ x^2 +2x+1=8x−4 ⇒ x^2 −6x+5=0 x_1 =1 and x_2 =5 S_R ={1,5}.

$${x}\geqslant−\frac{\mathrm{1}}{\mathrm{3}}\:{and}\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$${we}\:{have}\:\sqrt{\mathrm{3}{x}+\mathrm{1}}=\mathrm{1}+\sqrt{\mathrm{2}{x}−\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{3}{x}+\mathrm{1}=\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}{x}−\mathrm{1}}+\mathrm{2}{x}−\mathrm{1} \\ $$$$\Rightarrow\:{x}+\mathrm{1}=\mathrm{2}\sqrt{\mathrm{2}{x}−\mathrm{1}} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}=\mathrm{8}{x}−\mathrm{4} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{1}\:{and}\:{x}_{\mathrm{2}} =\mathrm{5} \\ $$$${S}_{\mathbb{R}} =\left\{\mathrm{1},\mathrm{5}\right\}. \\ $$

Answered by Rasheed.Sindhi last updated on 08/Sep/21

≡An Alternative≡ (√(3x+1)) − (√(2x−1)) =1 ⇒ p−q=1 p^2 −q^2 =(3x+1)−(2x−1)=x+2 (p−q)(p+q)=x+2 p+q=x+2 p−q=1 2p=x+3⇒p=((x+3)/2) 2q=x+1⇒q=((x+1)/2) p=(√(3x+1))=((x+3)/2) 4(3x+1)=x^2 +6x+9 x^2 −6x+5=0 (x−1)(x−5)=0 x=1,5 On verification it can be verified that both roots are true. (Same result can be obtained by q=(√(2x−1)) =((x+1)/2) 4(2x−1)=x^2 +2x+1 x^2 −6x+5=0)

$$\equiv\mathbb{A}\mathrm{n}\:\mathbb{A}\mathrm{lternative}\equiv \\ $$$$\sqrt{\mathrm{3}{x}+\mathrm{1}}\:−\:\sqrt{\mathrm{2}{x}−\mathrm{1}}\:=\mathrm{1} \\ $$$$\:\Rightarrow\:{p}−{q}=\mathrm{1} \\ $$$${p}^{\mathrm{2}} −{q}^{\mathrm{2}} =\left(\mathrm{3}{x}+\mathrm{1}\right)−\left(\mathrm{2}{x}−\mathrm{1}\right)={x}+\mathrm{2} \\ $$$$\left({p}−{q}\right)\left({p}+{q}\right)={x}+\mathrm{2} \\ $$$${p}+{q}={x}+\mathrm{2} \\ $$$${p}−{q}=\mathrm{1} \\ $$$$\mathrm{2}{p}={x}+\mathrm{3}\Rightarrow{p}=\frac{{x}+\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{2}{q}={x}+\mathrm{1}\Rightarrow{q}=\frac{{x}+\mathrm{1}}{\mathrm{2}} \\ $$$${p}=\sqrt{\mathrm{3}{x}+\mathrm{1}}=\frac{{x}+\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{4}\left(\mathrm{3}{x}+\mathrm{1}\right)={x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{1},\mathrm{5} \\ $$$${On}\:{verification}\:{it}\:{can}\:{be}\:{verified} \\ $$$${that}\:{both}\:{roots}\:{are}\:{true}. \\ $$$$ \\ $$$$\left({Same}\:{result}\:{can}\:{be}\:{obtained}\right. \\ $$$${by} \\ $$$${q}=\sqrt{\mathrm{2}{x}−\mathrm{1}}\:=\frac{{x}+\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{4}\left(\mathrm{2}{x}−\mathrm{1}\right)={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}=\mathrm{0}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply