Question Number 153513 by yeti123 last updated on 08/Sep/21
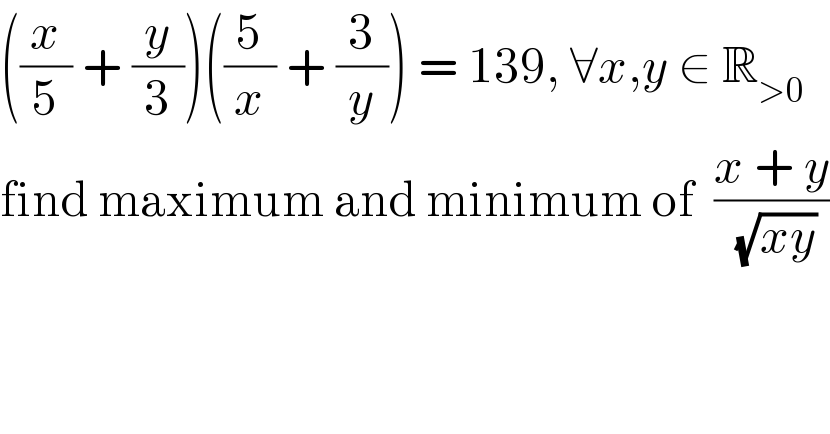
$$\left(\frac{{x}}{\mathrm{5}}\:+\:\frac{{y}}{\mathrm{3}}\right)\left(\frac{\mathrm{5}}{{x}}\:+\:\frac{\mathrm{3}}{{y}}\right)\:=\:\mathrm{139},\:\forall{x},{y}\:\in\:\mathbb{R}_{>\mathrm{0}} \\ $$$$\mathrm{find}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum}\:\mathrm{of}\:\:\frac{{x}\:+\:{y}}{\:\sqrt{{xy}}} \\ $$
Answered by liberty last updated on 08/Sep/21

$$\Rightarrow\frac{{x}+{y}}{\:\sqrt{{xy}}}\:=\:\sqrt{\frac{{x}}{{y}}}+\sqrt{\frac{{y}}{{x}}}=\sqrt{\frac{\mathrm{5}\lambda}{\mathrm{3}}}+\sqrt{\frac{\mathrm{3}}{\mathrm{5}\lambda}} \\ $$$${from}\:{condition} \\ $$$$\mathrm{2}+\frac{\mathrm{3}{x}}{\mathrm{5}{y}}+\frac{\mathrm{5}{y}}{\mathrm{3}{x}}\:=\mathrm{139} \\ $$$$\frac{\mathrm{3}{x}}{\mathrm{5}{y}}+\frac{\mathrm{5}{y}}{\mathrm{3}{x}}=\mathrm{137}\:{set}\:\frac{\mathrm{3}{x}}{\mathrm{5}{y}}=\lambda\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{5}\lambda}{\mathrm{3}} \\ $$$$\lambda+\frac{\mathrm{1}}{\lambda}=\mathrm{137}\Rightarrow\lambda^{\mathrm{2}} −\mathrm{137}\lambda+\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{137}\:\pm\sqrt{\left(\mathrm{137}+\mathrm{2}\right)\left(\mathrm{137}−\mathrm{2}\right)}}{\mathrm{2}} \\ $$$$\lambda=\frac{\mathrm{137}\pm\mathrm{136}.\mathrm{98}}{\mathrm{2}}\:\rightarrow\begin{cases}{\lambda_{\mathrm{1}} =\mathrm{136}.\mathrm{99}}\\{\lambda_{\mathrm{2}} =\mathrm{0}.\mathrm{007}}\end{cases} \\ $$$${f}\left(\lambda_{\mathrm{1}} \right)=\sqrt{\frac{\mathrm{5}×\mathrm{136}.\mathrm{99}}{\mathrm{3}}}+\sqrt{\frac{\mathrm{3}}{\mathrm{5}×\mathrm{136}.\mathrm{99}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{15}.\mathrm{176}\:\left({max}\right) \\ $$$${f}\left(\lambda_{\mathrm{2}} \right)=\sqrt{\frac{\mathrm{5}×\mathrm{0}.\mathrm{007}}{\mathrm{3}}}+\sqrt{\frac{\mathrm{3}}{\mathrm{5}×\mathrm{0}.\mathrm{07}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\approx\:\mathrm{9}.\mathrm{366}\:\left({min}\right) \\ $$
Commented by yeti123 last updated on 08/Sep/21

$$\mathrm{ok},\:\mathrm{thanks} \\ $$
Commented by MJS_new last updated on 08/Sep/21

$$\mathrm{you}\:\mathrm{should}\:\mathrm{round}\:\mathrm{significant}\:\mathrm{figures} \\ $$$$\lambda_{\mathrm{1}} \approx\mathrm{136}.\mathrm{99} \\ $$$$\lambda_{\mathrm{2}} \approx.\mathrm{0072997} \\ $$$$\Rightarrow \\ $$$${f}\left(\lambda_{\mathrm{1}} \right)\approx\mathrm{15}.\mathrm{176} \\ $$$${f}\left(\lambda_{\mathrm{2}} \right)\approx\mathrm{9}.\mathrm{1765} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{your}\:\mathrm{path}\:\mathrm{is}\:\mathrm{ok}\:\mathrm{but}\:\mathrm{your}\:\mathrm{2}^{\mathrm{nd}} \\ $$$$\mathrm{result}\:\mathrm{is}\:\mathrm{not}… \\ $$
Commented by liberty last updated on 08/Sep/21

Commented by liberty last updated on 08/Sep/21

$${o}\:{yes}… \\ $$
Answered by MJS_new last updated on 08/Sep/21
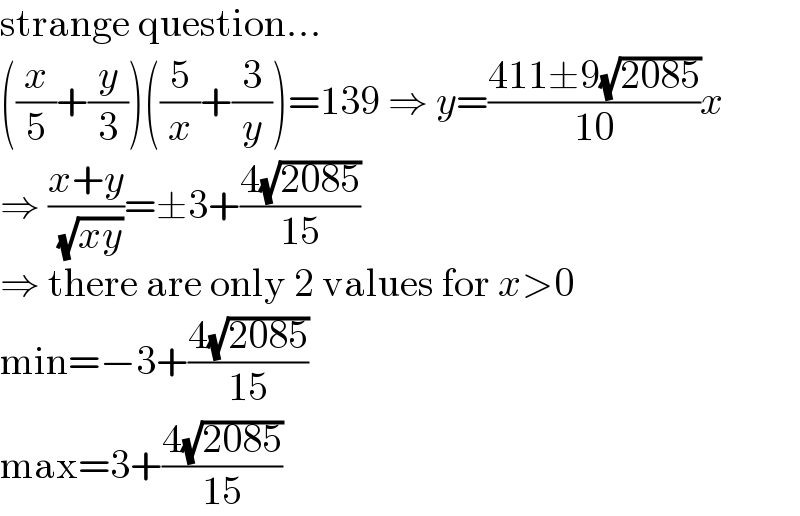
$$\mathrm{strange}\:\mathrm{question}… \\ $$$$\left(\frac{{x}}{\mathrm{5}}+\frac{{y}}{\mathrm{3}}\right)\left(\frac{\mathrm{5}}{{x}}+\frac{\mathrm{3}}{{y}}\right)=\mathrm{139}\:\Rightarrow\:{y}=\frac{\mathrm{411}\pm\mathrm{9}\sqrt{\mathrm{2085}}}{\mathrm{10}}{x} \\ $$$$\Rightarrow\:\frac{{x}+{y}}{\:\sqrt{{xy}}}=\pm\mathrm{3}+\frac{\mathrm{4}\sqrt{\mathrm{2085}}}{\mathrm{15}} \\ $$$$\Rightarrow\:\mathrm{there}\:\mathrm{are}\:\mathrm{only}\:\mathrm{2}\:\mathrm{values}\:\mathrm{for}\:{x}>\mathrm{0} \\ $$$$\mathrm{min}=−\mathrm{3}+\frac{\mathrm{4}\sqrt{\mathrm{2085}}}{\mathrm{15}} \\ $$$$\mathrm{max}=\mathrm{3}+\frac{\mathrm{4}\sqrt{\mathrm{2085}}}{\mathrm{15}} \\ $$
Commented by liberty last updated on 08/Sep/21

$$\:\mathrm{3}+\frac{\mathrm{4}\sqrt{\mathrm{2085}}}{\mathrm{15}}\:=\:\mathrm{15}.\mathrm{176} \\ $$
Commented by MJS_new last updated on 08/Sep/21

$$\mathrm{no}. \\ $$$$\approx\mathrm{15}.\mathrm{176} \\ $$
Commented by liberty last updated on 08/Sep/21
����������
Commented by yeti123 last updated on 08/Sep/21
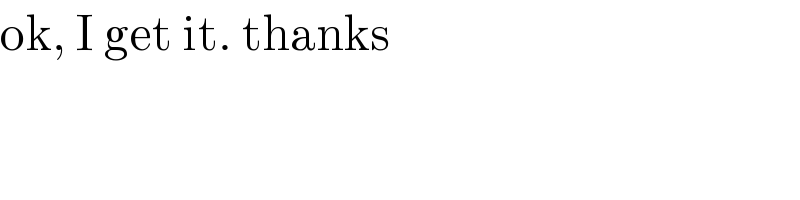
$$\mathrm{ok},\:\mathrm{I}\:\mathrm{get}\:\mathrm{it}.\:\mathrm{thanks} \\ $$
