Question Number 88169 by jagoll last updated on 08/Apr/20

$$\mathrm{find}\:\mathrm{Laplace}\:\mathrm{transform}\: \\ $$$$\mathrm{t}^{\mathrm{3}} .\:\mathrm{cos}\:\:\mathrm{4t} \\ $$
Commented by mathmax by abdo last updated on 08/Apr/20
![L(x^3 cos(4x))=∫_0 ^∞ f(t) e^(−xt) dt =∫_0 ^∞ t^3 cos(4t)e^(−xt) dt =Re(∫_0 ^∞ t^3 e^(i4t−xt) dt) ∫_0 ^∞ t^3 e^((−x+4i)t) dt =_(bypsrts) [(t^3 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 3t^2 e^((−x+4i)t) dt =(3/(x−4i)) { [(t^2 /(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ 2t e^((−x+4i)t) dt} =(6/((x−4i)^2 )) ∫_0 ^∞ t e^((−x+4i)t) dt =(6/((x−4i)^2 )){ [−(t/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ −(1/(−x+4i))∫_0 ^∞ e^((−x+4i)t) dt} =(6/((x−4i)^3 ))[(1/(−x+4i)) e^((−x+4i)t) ]_0 ^∞ =(6/((x−4i)^4 )) =6((1/(x−4i)))^4 =6(((x+4i)/(x^2 +16)))^4 =(6/(x^2 +16))(x+4i)^2 (x+4i)^2 =(6/(x^2 +16))(x^2 +8ix −16)^2 =(6/(x^2 +16)){ (x^2 +8ix)^2 −32(x^2 +8ix)+16^2 } =(6/(x^2 +16)){ x^4 +16ix^3 −64 x^2 −32x^2 −8.32ix +16^2 } ⇒ L(x^3 (4x)) =(6/(x^2 +16))( x^4 −96x^2 +16^2 )](https://www.tinkutara.com/question/Q88195.png)
$${L}\left({x}^{\mathrm{3}} {cos}\left(\mathrm{4}{x}\right)\right)=\int_{\mathrm{0}} ^{\infty} \:{f}\left({t}\right)\:{e}^{−{xt}} \:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} \:{cos}\left(\mathrm{4}{t}\right){e}^{−{xt}} \:{dt}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{t}^{\mathrm{3}} {e}^{{i}\mathrm{4}{t}−{xt}} \:{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} \:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \:{dt}\:=_{{bypsrts}} \:\:\:\left[\frac{{t}^{\mathrm{3}} }{−{x}+\mathrm{4}{i}}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{−{x}+\mathrm{4}{i}}\int_{\mathrm{0}} ^{\infty} \mathrm{3}{t}^{\mathrm{2}} \:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} {dt} \\ $$$$=\frac{\mathrm{3}}{{x}−\mathrm{4}{i}}\:\left\{\:\:\left[\frac{{t}^{\mathrm{2}} }{−{x}+\mathrm{4}{i}}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{−{x}+\mathrm{4}{i}}\int_{\mathrm{0}} ^{\infty} \mathrm{2}{t}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} {dt}\right\} \\ $$$$=\frac{\mathrm{6}}{\left({x}−\mathrm{4}{i}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:{t}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \:{dt}\: \\ $$$$=\frac{\mathrm{6}}{\left({x}−\mathrm{4}{i}\right)^{\mathrm{2}} }\left\{\:\left[−\frac{{t}}{−{x}+\mathrm{4}{i}}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \right]_{\mathrm{0}} ^{\infty} −\frac{\mathrm{1}}{−{x}+\mathrm{4}{i}}\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \:{dt}\right\} \\ $$$$=\frac{\mathrm{6}}{\left({x}−\mathrm{4}{i}\right)^{\mathrm{3}} }\left[\frac{\mathrm{1}}{−{x}+\mathrm{4}{i}}\:{e}^{\left(−{x}+\mathrm{4}{i}\right){t}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{6}}{\left({x}−\mathrm{4}{i}\right)^{\mathrm{4}} }\:=\mathrm{6}\left(\frac{\mathrm{1}}{{x}−\mathrm{4}{i}}\right)^{\mathrm{4}} \\ $$$$=\mathrm{6}\left(\frac{{x}+\mathrm{4}{i}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\right)^{\mathrm{4}} \:=\frac{\mathrm{6}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\left({x}+\mathrm{4}{i}\right)^{\mathrm{2}} \left({x}+\mathrm{4}{i}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{6}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\left({x}^{\mathrm{2}} +\mathrm{8}{ix}\:−\mathrm{16}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{6}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\left\{\:\left({x}^{\mathrm{2}} \:+\mathrm{8}{ix}\right)^{\mathrm{2}} −\mathrm{32}\left({x}^{\mathrm{2}} \:+\mathrm{8}{ix}\right)+\mathrm{16}^{\mathrm{2}} \right\} \\ $$$$=\frac{\mathrm{6}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\left\{\:{x}^{\mathrm{4}} \:+\mathrm{16}{ix}^{\mathrm{3}} −\mathrm{64}\:{x}^{\mathrm{2}} −\mathrm{32}{x}^{\mathrm{2}} −\mathrm{8}.\mathrm{32}{ix}\:+\mathrm{16}^{\mathrm{2}} \right\}\:\Rightarrow \\ $$$${L}\left({x}^{\mathrm{3}} \left(\mathrm{4}{x}\right)\right)\:=\frac{\mathrm{6}}{{x}^{\mathrm{2}} \:+\mathrm{16}}\left(\:{x}^{\mathrm{4}} −\mathrm{96}{x}^{\mathrm{2}} \:+\mathrm{16}^{\mathrm{2}} \right) \\ $$
Commented by mathmax by abdo last updated on 09/Apr/20
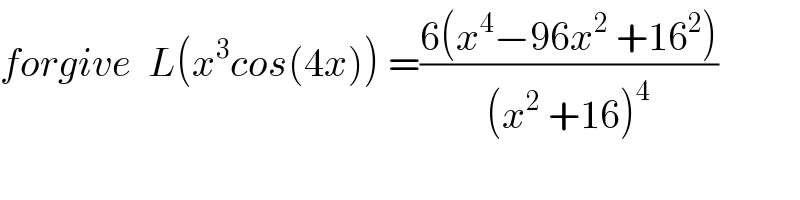
$${forgive}\:\:{L}\left({x}^{\mathrm{3}} {cos}\left(\mathrm{4}{x}\right)\right)\:=\frac{\mathrm{6}\left({x}^{\mathrm{4}} −\mathrm{96}{x}^{\mathrm{2}} \:+\mathrm{16}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} \:+\mathrm{16}\right)^{\mathrm{4}} } \\ $$
Answered by jagoll last updated on 09/Apr/20
![L(cos 4t) = (s/(s^2 +16)) L(t cos 4t) = −(d/ds)[(s/(s^2 +16))] = ((16−s^2 )/((s^2 +16)^2 )) L(t^2 cos 4t) = −(d/ds)[((16−s^2 )/((s^2 +16)^2 ))] = ((96s−2s^3 )/((s^2 +16)^3 )) L(t^3 cos 4t) = −(d/ds)[((96s−2s^3 )/((s^2 +16)^3 ))] = ((6(s^4 −96s^2 +256))/((s^2 +16)^4 ))](https://www.tinkutara.com/question/Q88205.png)
$$\mathrm{L}\left(\mathrm{cos}\:\mathrm{4t}\right)\:=\:\frac{\mathrm{s}}{\mathrm{s}^{\mathrm{2}} +\mathrm{16}} \\ $$$$\mathrm{L}\left(\mathrm{t}\:\mathrm{cos}\:\mathrm{4t}\right)\:=\:−\frac{\mathrm{d}}{\mathrm{ds}}\left[\frac{\mathrm{s}}{\mathrm{s}^{\mathrm{2}} +\mathrm{16}}\right]\:=\:\frac{\mathrm{16}−\mathrm{s}^{\mathrm{2}} }{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{16}\right)^{\mathrm{2}} } \\ $$$$\mathrm{L}\left(\mathrm{t}^{\mathrm{2}} \:\mathrm{cos}\:\mathrm{4t}\right)\:=\:−\frac{\mathrm{d}}{\mathrm{ds}}\left[\frac{\mathrm{16}−\mathrm{s}^{\mathrm{2}} }{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{16}\right)^{\mathrm{2}} }\right] \\ $$$$=\:\frac{\mathrm{96s}−\mathrm{2s}^{\mathrm{3}} }{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{16}\right)^{\mathrm{3}} } \\ $$$$\mathrm{L}\left(\mathrm{t}^{\mathrm{3}} \mathrm{cos}\:\mathrm{4t}\right)\:=\:−\frac{\mathrm{d}}{\mathrm{ds}}\left[\frac{\mathrm{96s}−\mathrm{2s}^{\mathrm{3}} }{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{16}\right)^{\mathrm{3}} }\right] \\ $$$$=\:\frac{\mathrm{6}\left(\mathrm{s}^{\mathrm{4}} −\mathrm{96s}^{\mathrm{2}} +\mathrm{256}\right)}{\left(\mathrm{s}^{\mathrm{2}} +\mathrm{16}\right)^{\mathrm{4}} } \\ $$
