Question Number 153765 by liberty last updated on 10/Sep/21

$$\:{Given}\:{f}:{R}\rightarrow{R}\:{is}\:{increasing}\:{positive} \\ $$$${function}\:{with}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}{x}\right)}{{f}\left({x}\right)}=\mathrm{1}\:.\: \\ $$$${What}\:{the}\:{value}\:{of}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}. \\ $$$$\left({A}\right)\:\mathrm{3}\:\:\:\:\:\left({B}\right)\:\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\:\:\left({C}\right)\:\mathrm{1}\:\:\:\:\:\left({D}\right)\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\left({E}\right)\:\infty \\ $$
Answered by gsk2684 last updated on 10/Sep/21
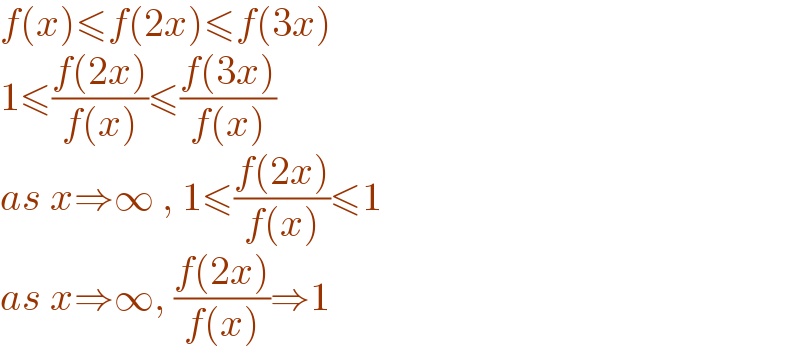
$${f}\left({x}\right)\leqslant{f}\left(\mathrm{2}{x}\right)\leqslant{f}\left(\mathrm{3}{x}\right) \\ $$$$\mathrm{1}\leqslant\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}\leqslant\frac{{f}\left(\mathrm{3}{x}\right)}{{f}\left({x}\right)} \\ $$$${as}\:{x}\Rightarrow\infty\:,\:\mathrm{1}\leqslant\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}\leqslant\mathrm{1} \\ $$$${as}\:{x}\Rightarrow\infty,\:\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}\Rightarrow\mathrm{1} \\ $$
Commented by liberty last updated on 10/Sep/21

$${thank}\:{you} \\ $$
Answered by puissant last updated on 10/Sep/21

$$\forall{x}\in\mathbb{R}, \\ $$$${x}\leqslant\mathrm{2}{x}\leqslant\mathrm{3}{x}\:\Rightarrow\:{f}\left({x}\right)\leqslant{f}\left(\mathrm{2}{x}\right)\leqslant{f}\left(\mathrm{3}{x}\right) \\ $$$$\left({because}\:{f}\:\nearrow\right). \\ $$$$\Rightarrow\:\mathrm{1}\leqslant\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}\leqslant\frac{{f}\left(\mathrm{3}{x}\right)}{{f}\left({x}\right)}\:\:\left({f}\left({x}\right)\neq\mathrm{0}\right).. \\ $$$$\Rightarrow\:\mathrm{1}\leqslant\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}\leqslant\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{f}\left(\mathrm{3}{x}\right)}{{f}\left({x}\right)}=\mathrm{1} \\ $$$$\left({Gendarm}\:{theorem}\right).. \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{f}\left(\mathrm{2}{x}\right)}{{f}\left({x}\right)}=\mathrm{1} \\ $$$$\left.{Answer}\::\:\:{C}\right) \\ $$
Commented by liberty last updated on 10/Sep/21
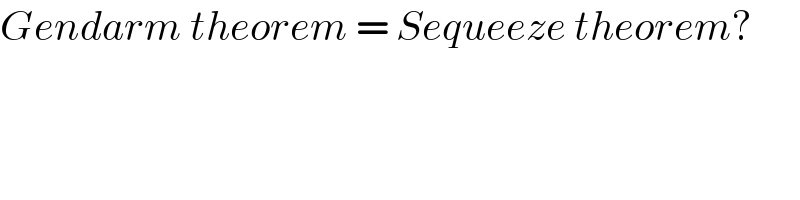
$${Gendarm}\:{theorem}\:=\:{Sequeeze}\:{theorem}? \\ $$
