Question Number 1999 by Fitrah last updated on 29/Oct/15
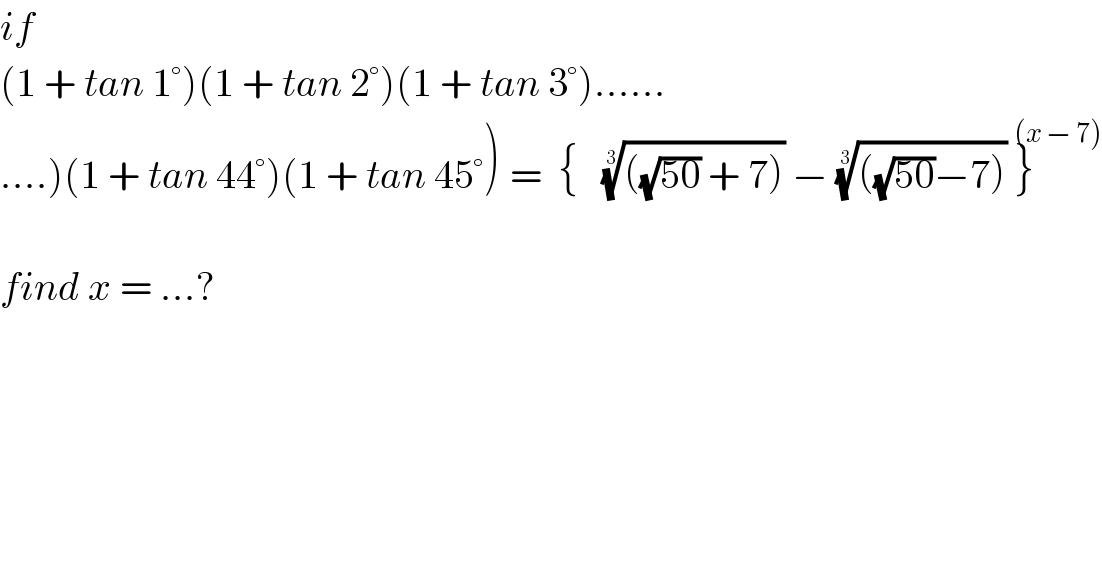
$${if}\: \\ $$$$\left(\mathrm{1}\:+\:{tan}\:\mathrm{1}°\right)\left(\mathrm{1}\:+\:{tan}\:\mathrm{2}°\right)\left(\mathrm{1}\:+\:{tan}\:\mathrm{3}°\right)…… \\ $$$$\left…..\right)\left(\mathrm{1}\:+\:{tan}\:\mathrm{44}°\right)\left(\mathrm{1}\:+\:{tan}\:\mathrm{45}°\right)\overset{} {\:}=\:\:\left\{\:\:\:\sqrt[{\mathrm{3}}]{\left(\sqrt{\mathrm{50}}\:+\:\mathrm{7}\right)}\:−\:\sqrt[{\mathrm{3}}]{\left(\sqrt{\mathrm{50}}−\mathrm{7}\right)}\:\overset{\left({x}\:−\:\mathrm{7}\right)} {\right\}} \\ $$$$\: \\ $$$${find}\:{x}\:=\:…? \\ $$
Answered by Yozzi last updated on 29/Oct/15
![The given equation can be written as d=c^(x−7) where c,d>0 since tan(r^° )>0 ∀r∈[1,45]⇒1+tan(r^° )>0 and (√(50))+7>(√(50))−7⇒((√(50))+7)^(1/3) >((√(50))−7)^(1/3) ⇒((√(50))+7)^(1/3) −((√(50))−7)^(1/3) >0. ∴ lnd=lnc^(x−7) ⇒lnd=(x−7)lnc ⇒x−7=((lnd)/(lnc))=log_c d x=7+log_c d x=7+log_((((√(50))+7)^(1/3) −((√(50))−7)^(1/3) )) (Π_(r=1) ^(45) (1+tan(r^° )))](https://www.tinkutara.com/question/Q2003.png)
$${The}\:{given}\:{equation}\:{can}\:{be}\:{written} \\ $$$${as}\:\:{d}={c}^{{x}−\mathrm{7}} \:{where}\:{c},{d}>\mathrm{0}\:{since} \\ $$$${tan}\left({r}^{°} \right)>\mathrm{0}\:\forall{r}\in\left[\mathrm{1},\mathrm{45}\right]\Rightarrow\mathrm{1}+{tan}\left({r}^{°} \right)>\mathrm{0} \\ $$$${and}\:\sqrt{\mathrm{50}}+\mathrm{7}>\sqrt{\mathrm{50}}−\mathrm{7}\Rightarrow\left(\sqrt{\mathrm{50}}+\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} >\left(\sqrt{\mathrm{50}}−\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\Rightarrow\left(\sqrt{\mathrm{50}}+\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} −\left(\sqrt{\mathrm{50}}−\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} >\mathrm{0}. \\ $$$$\therefore\:{lnd}={lnc}^{{x}−\mathrm{7}} \Rightarrow{lnd}=\left({x}−\mathrm{7}\right){lnc} \\ $$$$\Rightarrow{x}−\mathrm{7}=\frac{{lnd}}{{lnc}}={log}_{{c}} {d} \\ $$$${x}=\mathrm{7}+{log}_{{c}} {d} \\ $$$${x}=\mathrm{7}+{log}_{\left(\left(\sqrt{\mathrm{50}}+\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} −\left(\sqrt{\mathrm{50}}−\mathrm{7}\right)^{\mathrm{1}/\mathrm{3}} \right)} \left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\left(\mathrm{1}+{tan}\left({r}^{°} \right)\right)\right) \\ $$
Commented by Rasheed Soomro last updated on 29/Oct/15

$$\mathcal{V}{ery}\:\mathcal{N}{ice}! \\ $$
