Menu Close

Question-88286

Tinku Tara 0 Comments
Pin




Question Number 88286 by Chi Mes Try last updated on 09/Apr/20
Commented by abdomathmax last updated on 09/Apr/20
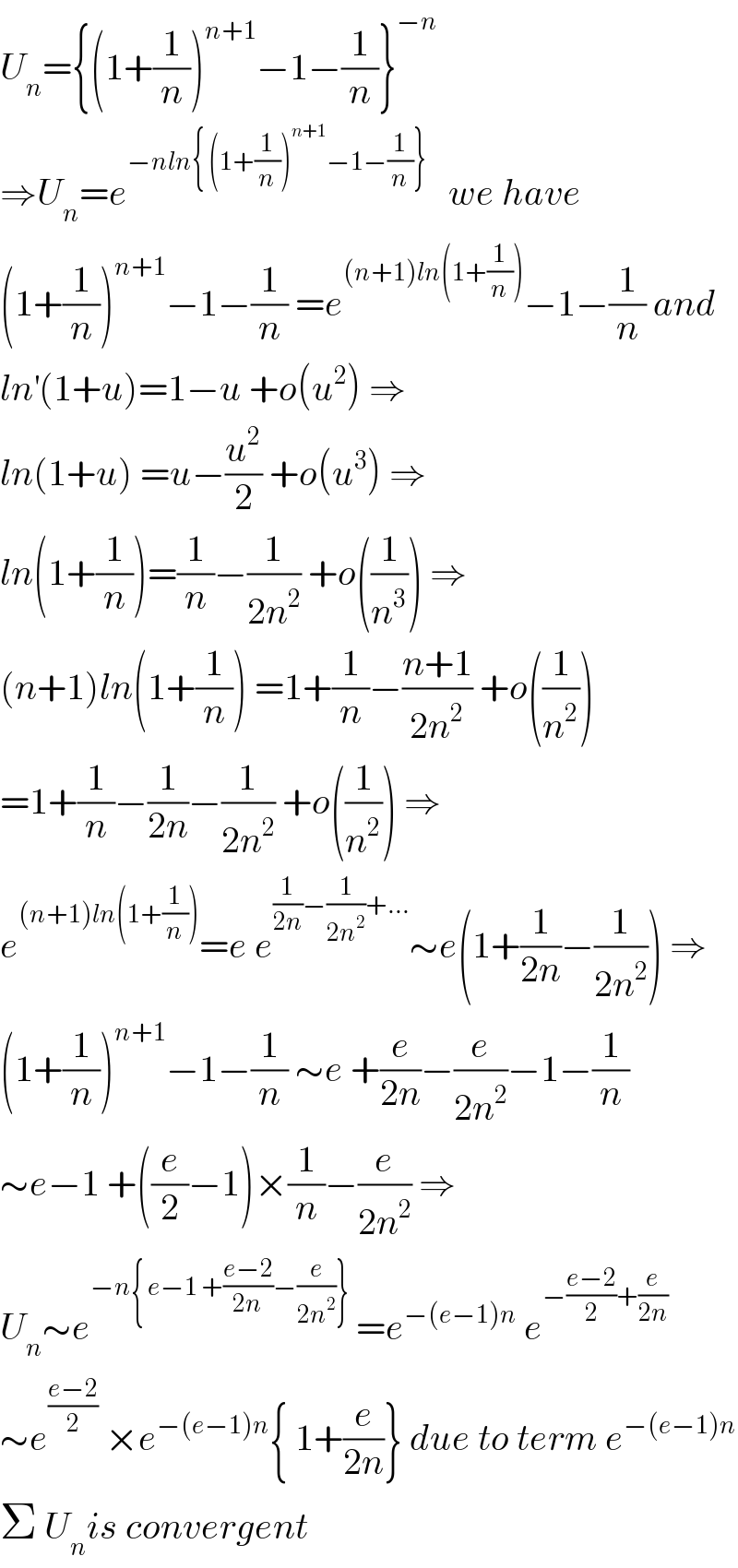
U_n ={(1+(1/n))^(n+1) −1−(1/n)}^(−n) ⇒U_n =e^(−nln{ (1+(1/n))^(n+1) −1−(1/n)} ) we have (1+(1/n))^(n+1) −1−(1/n) =e^((n+1)ln(1+(1/n))) −1−(1/n) and ln^′ (1+u)=1−u +o(u^2 ) ⇒ ln(1+u) =u−(u^2 /2) +o(u^3 ) ⇒ ln(1+(1/n))=(1/n)−(1/(2n^2 )) +o((1/n^3 )) ⇒ (n+1)ln(1+(1/n)) =1+(1/n)−((n+1)/(2n^2 )) +o((1/n^2 )) =1+(1/n)−(1/(2n))−(1/(2n^2 )) +o((1/n^2 )) ⇒ e^((n+1)ln(1+(1/n))) =e e^((1/(2n))−(1/(2n^2 ))+...) ∼e(1+(1/(2n))−(1/(2n^2 ))) ⇒ (1+(1/n))^(n+1) −1−(1/n) ∼e +(e/(2n))−(e/(2n^2 ))−1−(1/n) ∼e−1 +((e/2)−1)×(1/n)−(e/(2n^2 )) ⇒ U_n ∼e^(−n{ e−1 +((e−2)/(2n))−(e/(2n^2 ))}) =e^(−(e−1)n) e^(−((e−2)/2)+(e/(2n))) ∼e^((e−2)/2) ×e^(−(e−1)n) { 1+(e/(2n))} due to term e^(−(e−1)n) Σ U_n is convergent
$${U}_{{n}} =\left\{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{{n}}\right\}^{−{n}} \\ $$$$\Rightarrow{U}_{{n}} ={e}^{−{nln}\left\{\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{{n}}\right\}\:\:} \:\:{we}\:{have} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{{n}}\:={e}^{\left({n}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} −\mathrm{1}−\frac{\mathrm{1}}{{n}}\:{and} \\ $$$${ln}^{'} \left(\mathrm{1}+{u}\right)=\mathrm{1}−{u}\:+{o}\left({u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{u}\right)\:={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)=\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\:\Rightarrow \\ $$$$\left({n}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\:=\mathrm{1}+\frac{\mathrm{1}}{{n}}−\frac{{n}+\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${e}^{\left({n}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} ={e}\:{e}^{\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }+…} \sim{e}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}+\mathrm{1}} −\mathrm{1}−\frac{\mathrm{1}}{{n}}\:\sim{e}\:+\frac{{e}}{\mathrm{2}{n}}−\frac{{e}}{\mathrm{2}{n}^{\mathrm{2}} }−\mathrm{1}−\frac{\mathrm{1}}{{n}} \\ $$$$\sim{e}−\mathrm{1}\:+\left(\frac{{e}}{\mathrm{2}}−\mathrm{1}\right)×\frac{\mathrm{1}}{{n}}−\frac{{e}}{\mathrm{2}{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$${U}_{{n}} \sim{e}^{−{n}\left\{\:{e}−\mathrm{1}\:+\frac{{e}−\mathrm{2}}{\mathrm{2}{n}}−\frac{{e}}{\mathrm{2}{n}^{\mathrm{2}} }\right\}} \:={e}^{−\left({e}−\mathrm{1}\right){n}} \:{e}^{−\frac{{e}−\mathrm{2}}{\mathrm{2}}+\frac{{e}}{\mathrm{2}{n}}} \\ $$$$\sim{e}^{\frac{{e}−\mathrm{2}}{\mathrm{2}}} \:×{e}^{−\left({e}−\mathrm{1}\right){n}} \left\{\:\mathrm{1}+\frac{{e}}{\mathrm{2}{n}}\right\}\:{due}\:{to}\:{term}\:{e}^{−\left({e}−\mathrm{1}\right){n}} \\ $$$$\Sigma\:{U}_{{n}} {is}\:{convergent} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *