Question Number 153972 by SANOGO last updated on 12/Sep/21
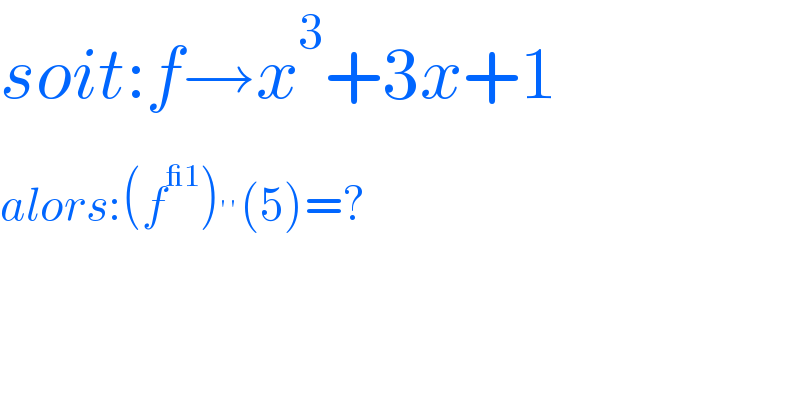
$${soit}:{f}\rightarrow{x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{1} \\ $$$${alors}:\left({f}^{\_\mathrm{1}} \right)^{''} \left(\mathrm{5}\right)=? \\ $$
Answered by mr W last updated on 12/Sep/21

$${f}\left({x}\right)={y}={x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{1} \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{1}−{y}=\mathrm{0} \\ $$$${x}=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{y}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{{y}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{y}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{{y}−\mathrm{1}}{\mathrm{2}}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{{x}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{{x}−\mathrm{1}}{\mathrm{2}}} \\ $$$$ \\ $$$$\mathrm{1}=\mathrm{3}{x}^{\mathrm{2}} \frac{{dx}}{{dy}}+\mathrm{3}\frac{{dx}}{{dy}}\:\Rightarrow\frac{{dx}}{{dy}}=\frac{\mathrm{1}}{\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{0}=\mathrm{6}{x}\left(\frac{{dx}}{{dy}}\right)^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }+\mathrm{3}\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} } \\ $$$$\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }=−\frac{\mathrm{2}{x}}{\mathrm{9}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow\left({f}^{−\mathrm{1}} \left({x}\right)\right)''=−\frac{\mathrm{2}{f}^{−\mathrm{1}} \left({x}\right)}{\mathrm{9}\left({f}^{−\mathrm{1}} \left({x}\right)^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${with}\:{f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{{x}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{{x}−\mathrm{1}}{\mathrm{2}}} \\ $$$${f}^{−\mathrm{1}} \left(\mathrm{5}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{1}+\left(\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\frac{\mathrm{5}−\mathrm{1}}{\mathrm{2}}} \\ $$$${f}^{−\mathrm{1}} \left(\mathrm{5}\right)=\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{5}}+\mathrm{2}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{5}}−\mathrm{2}}=\mathrm{1} \\ $$$$\left({f}^{−\mathrm{1}} \left(\mathrm{5}\right)\right)''=−\frac{\mathrm{2}×\mathrm{1}}{\mathrm{9}\left(\mathrm{1}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=−\frac{\mathrm{1}}{\mathrm{36}} \\ $$
Commented by SANOGO last updated on 12/Sep/21

$${merci}\:{bien}\:{le}\:{dur} \\ $$
Answered by mnjuly1970 last updated on 12/Sep/21

$$\:\:\:\left({f}^{−\mathrm{1}} \right)'\left(\mathrm{5}\:\right)=\frac{\:\mathrm{1}}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}}\:\mid_{\:{x}=\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\:\:\:\:\:{f}\:'\:\left({x}\right)=\:\mathrm{3}{x}^{\:\mathrm{2}} +\mathrm{3} \\ $$$$\:\:\:\:\:\:\left({f}\:^{−\mathrm{1}} \right)'\left({y}\:\right)=\frac{\mathrm{1}}{{f}\:'\left({x}\right)} \\ $$$$\:\:\:\:\:\:{y}'\:\left({f}^{\:−\mathrm{1}} \right)''\left({y}\:\right)=\:\frac{−{f}\:''\left({x}\right)}{{f}\:'^{\:\mathrm{2}} \left({x}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\left({f}\:^{−\mathrm{1}} \right)\left(\mathrm{5}\right)=\:=\frac{−\mathrm{6}}{\left({f}\:'\right)^{\:\mathrm{3}} \left(\mathrm{1}\right)}=\frac{−\mathrm{6}}{\mathrm{216}}\:=\:\frac{−\mathrm{1}}{\mathrm{36}} \\ $$
Commented by SANOGO last updated on 13/Sep/21

$${merci}\:{beaucoup}\:{le}\:{dur} \\ $$
