Question Number 88458 by TawaTawa1 last updated on 10/Apr/20
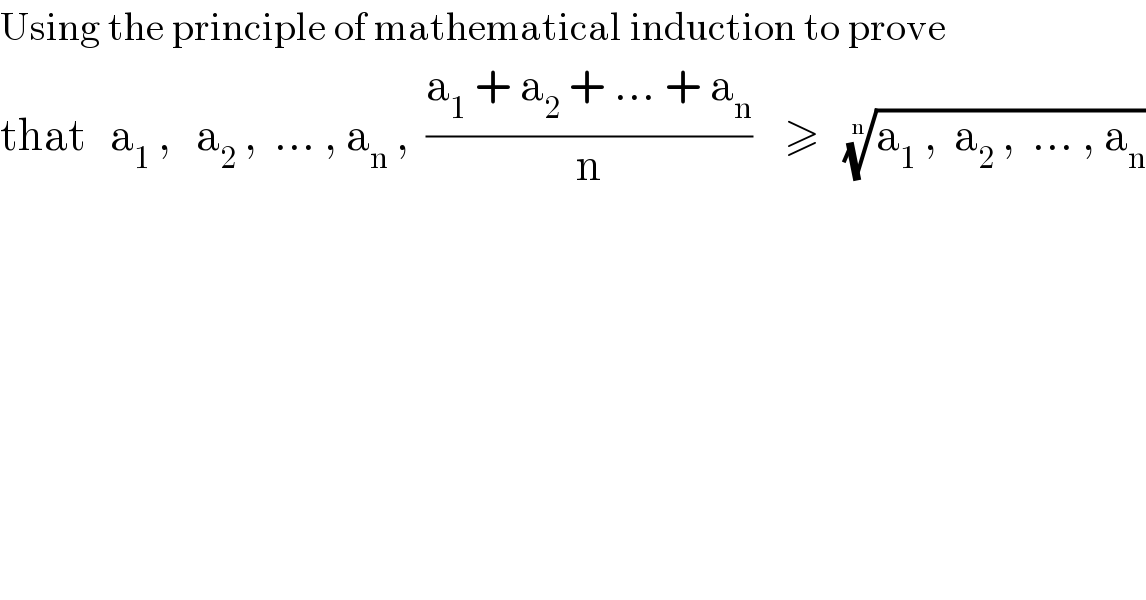
$$\mathrm{Using}\:\mathrm{the}\:\mathrm{principle}\:\mathrm{of}\:\mathrm{mathematical}\:\mathrm{induction}\:\mathrm{to}\:\mathrm{prove} \\ $$$$\mathrm{that}\:\:\:\mathrm{a}_{\mathrm{1}} \:,\:\:\:\mathrm{a}_{\mathrm{2}} \:,\:\:…\:,\:\mathrm{a}_{\mathrm{n}} \:,\:\:\frac{\mathrm{a}_{\mathrm{1}} \:+\:\mathrm{a}_{\mathrm{2}} \:+\:…\:+\:\mathrm{a}_{\mathrm{n}} }{\mathrm{n}}\:\:\:\:\geqslant\:\:\:\sqrt[{\mathrm{n}}]{\mathrm{a}_{\mathrm{1}} \:,\:\:\mathrm{a}_{\mathrm{2}} \:,\:\:…\:,\:\mathrm{a}_{\mathrm{n}} } \\ $$
