Question Number 22929 by selestian last updated on 24/Oct/17

Answered by ajfour last updated on 24/Oct/17
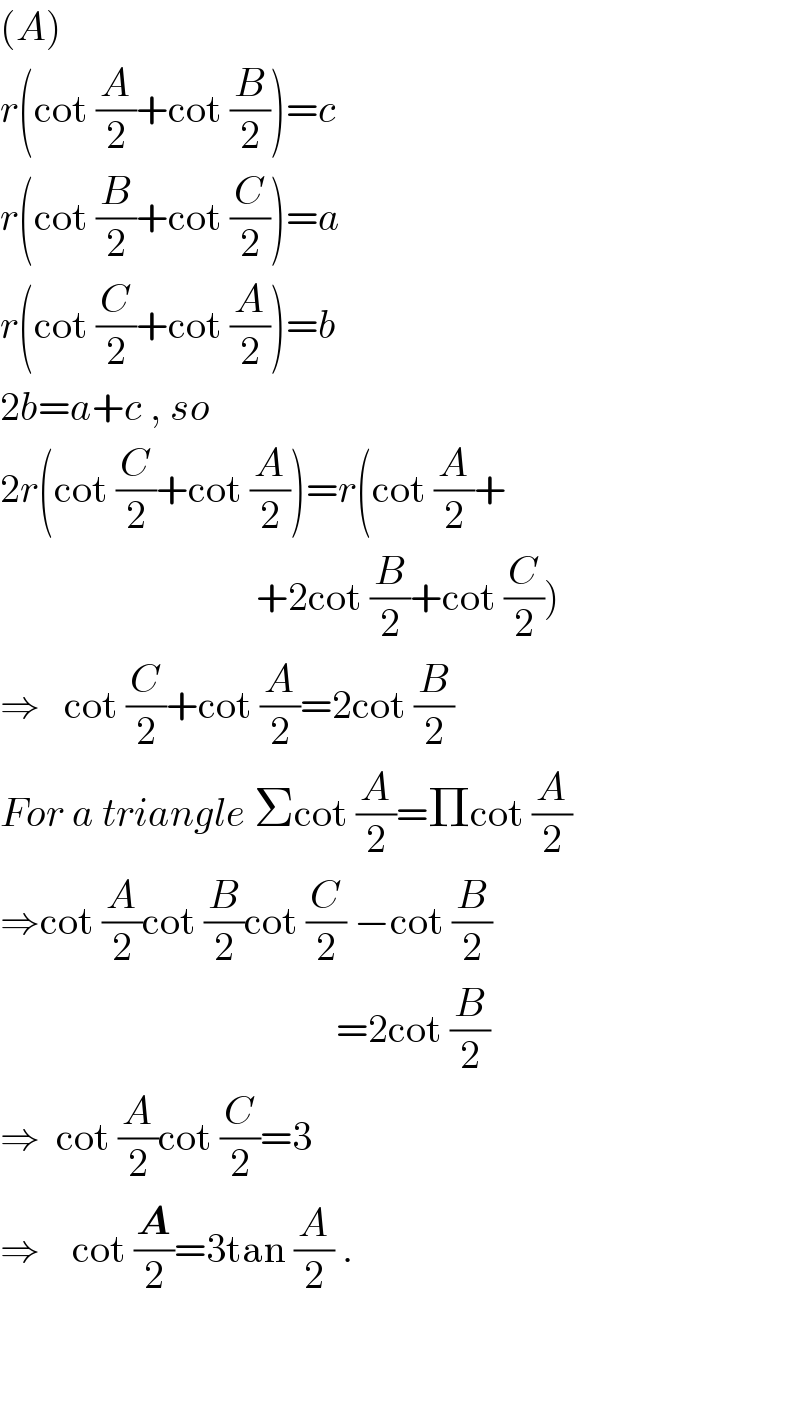
$$\left({A}\right) \\ $$$${r}\left(\mathrm{cot}\:\frac{{A}}{\mathrm{2}}+\mathrm{cot}\:\frac{{B}}{\mathrm{2}}\right)={c} \\ $$$${r}\left(\mathrm{cot}\:\frac{{B}}{\mathrm{2}}+\mathrm{cot}\:\frac{{C}}{\mathrm{2}}\right)={a} \\ $$$${r}\left(\mathrm{cot}\:\frac{{C}}{\mathrm{2}}+\mathrm{cot}\:\frac{{A}}{\mathrm{2}}\right)={b} \\ $$$$\mathrm{2}{b}={a}+{c}\:,\:{so} \\ $$$$\mathrm{2}{r}\left(\mathrm{cot}\:\frac{{C}}{\mathrm{2}}+\mathrm{cot}\:\frac{{A}}{\mathrm{2}}\right)={r}\left(\mathrm{cot}\:\frac{{A}}{\mathrm{2}}+\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2cot}\:\frac{{B}}{\mathrm{2}}+\mathrm{cot}\:\frac{{C}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{cot}\:\frac{{C}}{\mathrm{2}}+\mathrm{cot}\:\frac{{A}}{\mathrm{2}}=\mathrm{2cot}\:\frac{{B}}{\mathrm{2}} \\ $$$${For}\:{a}\:{triangle}\:\Sigma\mathrm{cot}\:\frac{{A}}{\mathrm{2}}=\Pi\mathrm{cot}\:\frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cot}\:\frac{{A}}{\mathrm{2}}\mathrm{cot}\:\frac{{B}}{\mathrm{2}}\mathrm{cot}\:\frac{{C}}{\mathrm{2}}\:−\mathrm{cot}\:\frac{{B}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2cot}\:\frac{{B}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{cot}\:\frac{{A}}{\mathrm{2}}\mathrm{cot}\:\frac{{C}}{\mathrm{2}}=\mathrm{3} \\ $$$$\Rightarrow\:\:\:\:\mathrm{cot}\:\frac{\boldsymbol{{A}}}{\mathrm{2}}=\mathrm{3tan}\:\frac{{A}}{\mathrm{2}}\:. \\ $$$$\:\:\:\: \\ $$$$ \\ $$
Commented by selestian last updated on 24/Oct/17

$${sir}\:{plz}\:{send}\:{me}\:{the}\:{solution}\:{plz}\:{plz} \\ $$$$ \\ $$
Commented by math solver last updated on 24/Oct/17
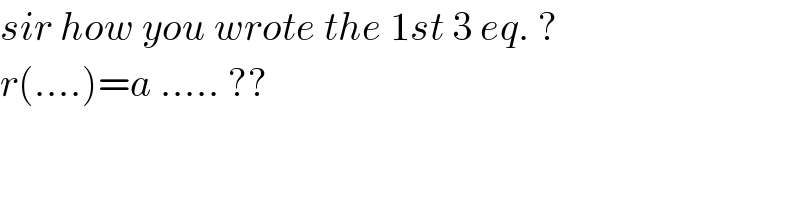
$${sir}\:{how}\:{you}\:{wrote}\:{the}\:\mathrm{1}{st}\:\mathrm{3}\:{eq}.\:? \\ $$$${r}\left(….\right)={a}\:…..\:?? \\ $$
Commented by ajfour last updated on 24/Oct/17
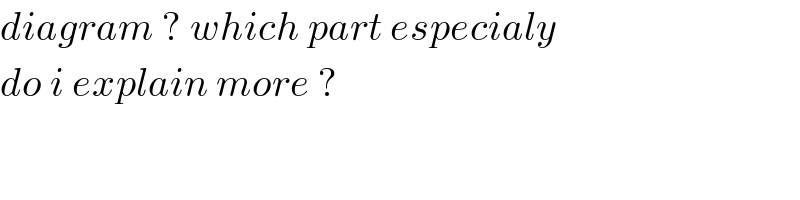
$${diagram}\:?\:{which}\:{part}\:{especialy} \\ $$$${do}\:{i}\:{explain}\:{more}\:? \\ $$
Commented by selestian last updated on 24/Oct/17
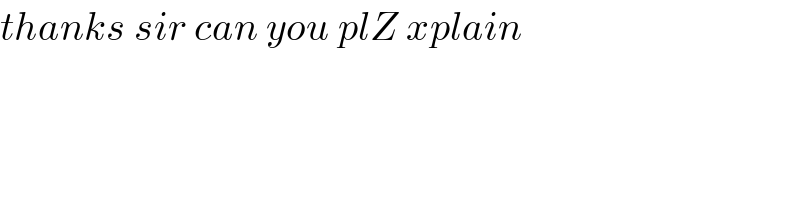
$${thanks}\:{sir}\:{can}\:{you}\:{plZ}\:{xplain} \\ $$
Commented by ajfour last updated on 25/Oct/17

$${see}\:{Q}.\mathrm{23009} \\ $$
Commented by selestian last updated on 25/Oct/17
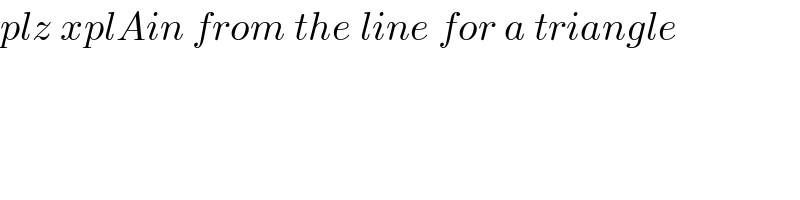
$${plz}\:{xplAin}\:{from}\:{the}\:{line}\:{for}\:{a}\:{triangle} \\ $$
