Question Number 88541 by ajfour last updated on 11/Apr/20
Commented by ajfour last updated on 11/Apr/20
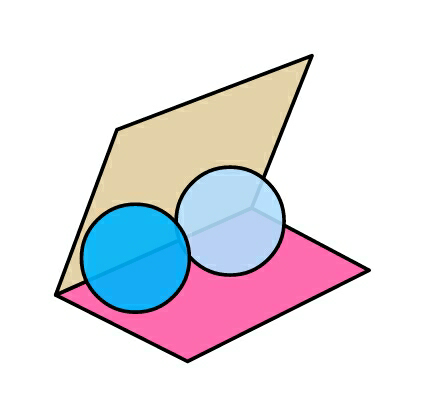
![The two shown spheres, each of radius r are tangent to each other and to the faces of a dihedral angle α. Find the radius of the sphere that is tangent to the planes and the two spheres as well. Ans: R= r[1+2tan^2 ((α/2))± tan ((α/2))(√(3+4tan^2 ((α/2)))) ]](https://www.tinkutara.com/question/Q88543.png)
$${The}\:{two}\:{shown}\:{spheres},\:{each}\:{of} \\ $$$${radius}\:{r}\:{are}\:{tangent}\:{to}\:{each}\:{other} \\ $$$${and}\:{to}\:{the}\:{faces}\:{of}\:{a}\:{dihedral}\: \\ $$$${angle}\:\alpha.\:{Find}\:{the}\:{radius}\:{of}\:{the} \\ $$$${sphere}\:{that}\:{is}\:{tangent}\:{to}\:{the} \\ $$$${planes}\:{and}\:{the}\:{two}\:{spheres}\:{as}\:{well}. \\ $$$${Ans}:\: \\ $$$${R}=\:{r}\left[\mathrm{1}+\mathrm{2tan}\:^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)\pm\:\mathrm{tan}\:\left(\frac{\alpha}{\mathrm{2}}\right)\sqrt{\mathrm{3}+\mathrm{4tan}\:^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}\right)}\:\right] \\ $$
Commented by ajfour last updated on 11/Apr/20
Commented by Ar Brandon last updated on 11/Apr/20
$${Which}\:{app}\:{permitted}\:{you}\:{to}\:{design} \\ $$$${this}\:{please}? \\ $$
Commented by ajfour last updated on 11/Apr/20

$${Lekh}\:{Diagram};\:{over}\:{time}\:{i}\:{am} \\ $$$${friendly}\:{with}\:{this}\:{app}.. \\ $$
Commented by Ar Brandon last updated on 02/May/20

$$\mathrm{thanks} \\ $$
Answered by mr W last updated on 11/Apr/20
Commented by mr W last updated on 11/Apr/20

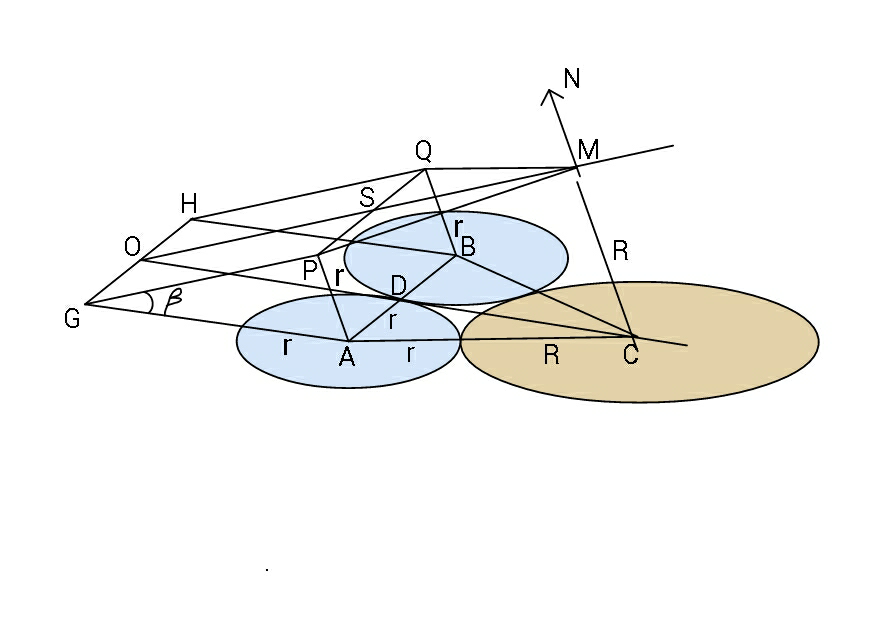
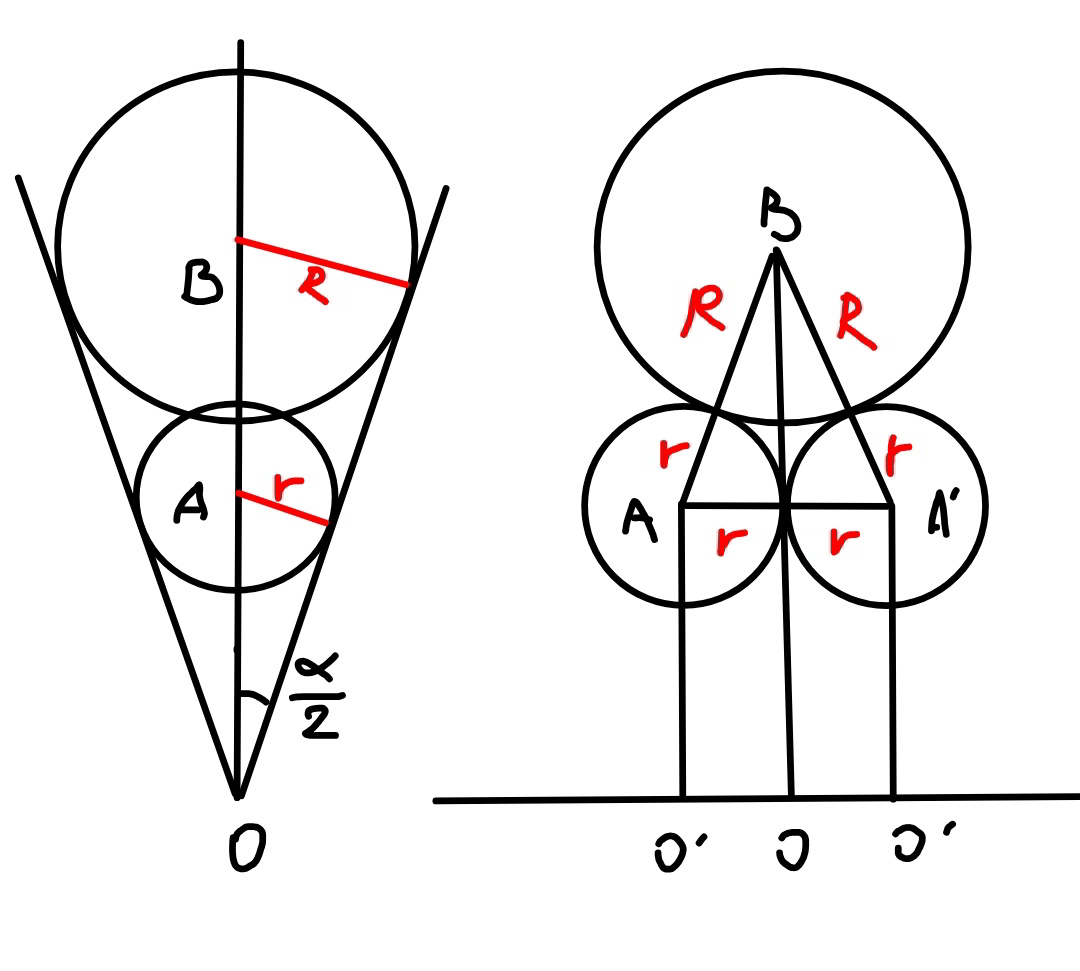
$${O}'{A}=\frac{{r}}{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}} \\ $$$${OB}=\frac{{R}}{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}} \\ $$$$\left({R}+{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\left(\frac{{R}}{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}−\frac{{r}}{\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)−\mathrm{2}{Rr}\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)+{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\pm\sqrt{\left(\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\right)}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\pm\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{3}+\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}} \\ $$$$\frac{{R}}{{r}}=\mathrm{1}+\mathrm{2}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}\pm\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\sqrt{\mathrm{3}+\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 11/Apr/20
$${oh}\:{yes},\:{this}\:{was}\:{too}\:{easy}\:{sir}, \\ $$$${i}\:{had}\:{expected}\:{it}\:{to}\:{be}\:{somewhat} \\ $$$${difficult};\:{thanks}\:{Sir}. \\ $$
