Question Number 88586 by M±th+et£s last updated on 11/Apr/20
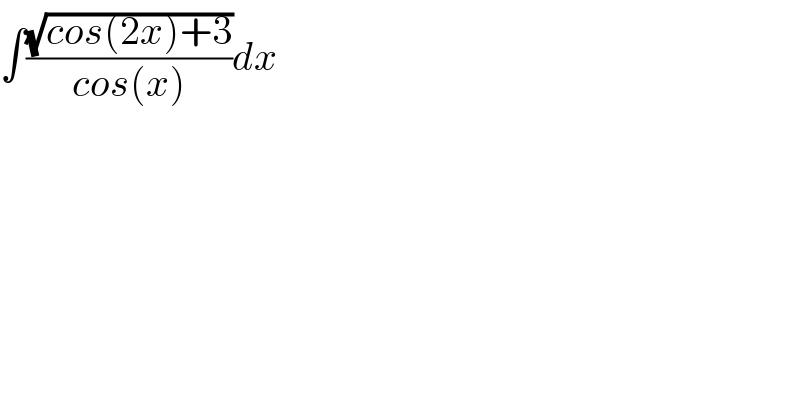
$$\int\frac{\sqrt{{cos}\left(\mathrm{2}{x}\right)+\mathrm{3}}}{{cos}\left({x}\right)}{dx} \\ $$
Answered by TANMAY PANACEA. last updated on 11/Apr/20

$$\int\frac{{cos}\mathrm{2}{x}+\mathrm{3}}{{cosx}\sqrt{\mathrm{3}+{cos}\mathrm{2}{x}}}{dx} \\ $$$$\int\frac{\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{2}}{{cosx}\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{2}}} \\ $$$$\frac{{I}}{\mathrm{2}}=\int\frac{{cosx}}{\:\sqrt{\mathrm{2}\left({cos}^{\mathrm{2}} {x}+\mathrm{1}\right)}}{dx}+\int\frac{{secx}\:{dx}}{\:\sqrt{\mathrm{2}{cos}^{\mathrm{2}} {x}+\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{cosx}}{\:\sqrt{\mathrm{2}−{sin}^{\mathrm{2}} {x}}}{dx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{sec}^{\mathrm{2}} {x}\:{dx}}{\:\sqrt{\mathrm{1}+{sec}^{\mathrm{2}} {x}}} \\ $$$$\frac{{I}}{\:\sqrt{\mathrm{2}}}=\int\frac{{d}\left({sinx}\right)}{\:\sqrt{\mathrm{2}−{sin}^{\mathrm{2}} {x}}}+\int\frac{{d}\left({tanx}\right)}{\:\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {x}}} \\ $$$${I}=\sqrt{\mathrm{2}}\:\left[{sin}^{−\mathrm{1}} \left(\frac{{sinx}}{\:\sqrt{\mathrm{2}}}\right)+{ln}\left({tanx}+\sqrt{\mathrm{2}+{tan}^{\mathrm{2}} {x}}\:\right)\right. \\ $$$${pls}\:{check} \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 11/Apr/20
$${correct}\:{solution}\:{thank}\:{you}\:{sir} \\ $$
